|

On this page we describe an unsolved problem in geometry dealing
with reflected triangles. [This problem was solved in 2012 by Grégoire Nicollier. A complete solution is in his paper that appears in Forum Geometricorum.] This problem led to the above graphic, which
is also the background image on the Mathematicians at Work poster.
When Judi and Harley were looking for a background for the poster,
Nathalie introduced them to this problem and the algorithm that produced
the graphic.
Start with triangle ABC and reflect each vertex across the opposite side;
you get triangle A1B1C1— the first
reflected triangle.
What is the relationship between the triangles ABC and A1B1C1?
When ABC is isosceles, so is A1B1C1
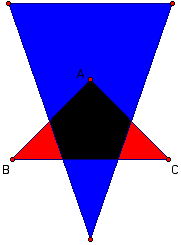
and when ABC is equilateral, so is A1B1C1.
You might want to verify these two statements by yourself. Suppose now that we fix the
position of B and C, but move A to change the shape of the original triangle
ABC. Then the shape of A1B1C1 changes
also. If your browser has java enabled you can open
a new window that allows you to move A, B or C and observe how the reflected
triangle changes.
Of the two triangles ABC and A1B1C1, it is often the second that looks more like an equilateral triangle. To get a sense of “how
close to being equilateral” it is, we need a measure. There are
many measures we can use: we could measure how far the angles are
from being
60 degrees, or how far the lengths of the sides are from being equal.
The measure we are going to use is the ratio of the perimeter squared
to the area. This ratio is at a minimum for an equilateral triangle (see,
for example, Kazarinoff). The minimum is 12  sqrt(3),
which is approximately 20.7. sqrt(3),
which is approximately 20.7.
In addition to looking at the triangle A1B1C1 generated
by reflecting the vertices of ABC, we want to reflect the vertices of
A1B1C1 to generate a second
reflected triangle A2B2C2. Then using
the vertices of A2B2C2 we generate
a third reflected triangle A3B3C3,
then a fourth, and so on. We call these the first, second, third and
fourth
iterations of the reflection process. Here are some pictures of three
iterations starting with A in different positions. Again, if your browser
has java enabled you can open
a new window that allows you to move A and observe how the reflected
triangles change.
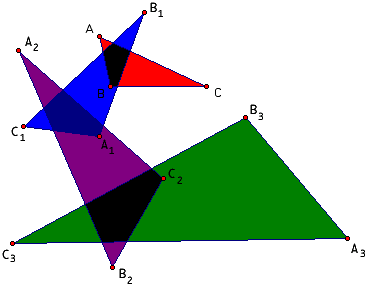
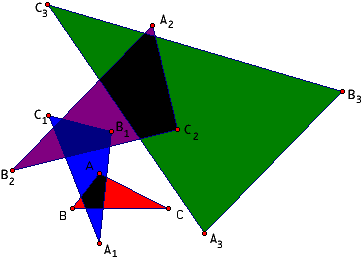
Originally it was conjectured that whatever the triangle
ABC, the sequence of triangles A1B1C1,
A2B2C2, A3B3C3,…
would always approach an equilateral triangle (Schwartz). As is usually
the case with mathematical research, people began looking for either
a
proof of the conjecture or a counterexample to the conjecture. Keith
Dean showed that a triangle with angles in the ratios of 1:2:4 (that with angles that measure 25 5/7, 51 3/7 and 102 6/7 degrees respectively)
reflects into another triangle with the same angles, and hence repeated
reflections will never
produce an equilateral triangle. Thus the conjecture is false. Patrick
Callaghan also found a characterization of the triangles that will map
onto a straight line. For these triangles also, the conjecture is false.
Thus the problem is:
“For what triangles ABC does the sequence
of iterated triangles approach an equilateral triangle?”
Nathalie devised a procedure for “seeing” many cases
at once. This is the procedure used to produce the background graphic
on the Mathematicians at Work poster.
Fix the base of the triangle BC,
chose another point A in the plane to form the triangle ABC, perform
the reflection twice
to produce
A2B2C2 and then colour the point A
according to how close A2B2C2 is to
being equilateral. A is painted blue if A2B2C2 is
close to being equilateral and white if A2B2C2 is
far from being equilateral. This procedure is repeated for all points
A in a rectangular region in the plane to generate the graphic below.

Two iterations1
There are large regions in the graphic that are
coloured blue. If A is in one of these regions then A2B2C2 is
close to being equilateral. There are, however, regions coloured white.
If A is in one of these regions then A2B2C2 is
far from being equilateral.
If the reflection is iterated three times to produce A3B3C3
and A is coloured according to how close A3B3C3
is to being equilateral, then the resulting image below is similar to
that above, but with a more complex pattern in the white regions.

Three iterations1
Similarly, the graphic below, which was produced by four
iterations, has even more blue and less white. We can infer from this
that as we increase the number of iterations, more of the initial triangles
have a final reflected triangle that is close to being equilateral.

Four iterations1
At this stage, we can reflect some more on what we are
seeing. If we do enough iterations, will the entire picture be blue?
It shouldn't, we know that there are some triangles (described above)
that do not converge to equilateral triangles. Regions corresponding
to these
triangles
should
stay white. You can use the java applets above to discover some positions
for A that seem to result in triangles that converge to a line. Why are
there other regions that are white? Can you find other conditions/positions
for A that will result in a sequence of triangles that doesn't converge
to an equilateral triangle? Do these images help in addressing the original
question; for what triangles ABC does the sequence of iterated
triangles approach an equilateral triangle? Computer graphics can give
insight into answering these questions but a complete answer requires
a mathematical proof.
If you
find something interesting in your explorations of these questions,
please let us know at  .
Maybe your name can be added to the list of people who have made contributions
towards a solution of this
problem. .
Maybe your name can be added to the list of people who have made contributions
towards a solution of this
problem.
In August of 2006 we received this note from Pasquale Nardone, Université Libre de Bruxelles.
1 Graphics produced
by Matthew McKague
- References
-
- Judah Schwartz, "Can technology help us make the mathematics
curriculum intellectually stimulating and socially responsible?"
International Journal of Computers for Mathematical Learning, 4,1999,
pages 99-119.
Nicholas D. Kazarinoff, Geometric Inequalities, Random House,
New York, 1961.
| 
