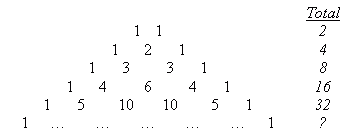I am a high school student, my teacher gave the class a worksheet on permutations and probability and told us to do independent work when we have not covered the material yet and he will not answer any questions. I am lost and don’t know where to begin. Can you help?

1. Find the number of 6-letter permutations of all the letters in EUCLID that end with either the letter E or the letter D?

Aluminum chips A, B. C, and D weigh 1g. 5g. 10g. and 20g. respectively. How many different masses can be measured by using one or more of the 4 weighs on a balance scale?

I appreciate any explanation that you can provide. He told us to find out how to do this on our own. Great.

Thank you
Alyssa

The first question is just asking how many ways you can order those six letters in such a way that the last letter is a D or an E. One example is EUCLID, another is DULCIE, another is LCIDUE and so on. There are a couple of ways of solving this problem.

a) Figure out how many ways there are of arranging the six letters, then multiply that by 2/6 (because only 2 of the six letters can be the last letter) or

b) Figure out how many ways there are of arranging five letters + E. If you double that (because of the five letters + D alternative), you get the answer.

Let's do (b) and check out answer with (a):

If we put the letters U,C,L,I,D in a heap and randomly choose one from the five, there are five possibilities. We put that letter first. Now we choose another letter from the heap of four. There are four possibilities. There were five choices for the first letter, only four for the second letter and you can predict, three, two and one for the third, fourth and fifth letters. Now comes the most important part: When you have various possibilities for a bunch of different variables, you multiply them together to figure out the number of possibilities in all. So 5 x 4 x 3 x 2 x 1 = 120. So there are 120 ways we can arrange the letters U,C,L,I,D. In all cases, we just leave an E on the end. Now if we double that for the alternative of keeping the D on the end and arranging E,U,C,L,I, then there are 240 variations in all.

Let's check with (a): Start with a pile of all six letters. If you choose them one after another you get 6 x 5 x 4 x 3 x 2 x 1 = 720. But remember that this treats all letters equally, so each of the six letters has equal odds of being the last letter. Since you want just a D or E, that's 2/6, and 720 x 2/6 = 240. The same answer.

Your second question regarding masses is a doesn't really care about order. Permutations are the possibilities when order counts (like your first question) and Combinations are the possibilities when order doesn't count (like choosing a group of weights).

Think about the weights like this: You can choose no weights at all, or one weight, or two, or three or all four. If you choose one or two or three, which ones you choose matters: Choose 1g+5g is different from 20g+5g, but choosing 10g+5g is the same as 5g+10g.

One way of solving this problem is to count each number of weights:
0 weights: one choice
1 weight: four choices (1g, 5g, 10g, 20g)
2 weights: six choices (1+5, 1+10, 1+20, 5+10, 5+20, 10+20)
3 weights: four choices (5+10+20, 1+10+20, 1+5+20, 1+5+10)
4 weights: one choice.
Add this up and you get 1+4+6+4+1 = 16.

But there's a better way of solving this too. Let's look at a simpler problem: What if there was no 20g weight? Then your table of choices would be:
0 weights: one choice (none)
1 weight: three choices (1, 5, 10)
2 weights: three choices (1+5, 1+10, 5+10)
3 weights: one choice (all)
That's 1+3+3+1 = 8.

If there were just the 1g and 5g weights, we'd have:
0 weights: one choice (none)
1 weight: two choices (1, 5)
2 weights: once choice (all)
That's 1+2+1 = 4.

And just the 1g weight?
0 weights: one choice (none)
1 weight: one choice (all)
1+1=2.

Okay, you say "this is pretty obvious - what's your point?" Have you ever heard of Pascal's Triangle?

It's a remarkable triangle that shows all these numbers and predicts the same for other amounts of weights. Here is the top of the triangle and the totals of the numbers in each row:

Do you see any pattern? Each total is double the previous total. That's 2^r if you write it as a number with r as the row number. The way that Pascal's triangle is constructed, the edges are all ones, but the inner numbers are the sum of the two numbers above them (for example, the 6 = 3 + 3, the numbers above the six).

Now here's another useful way to solve the problem:
You either use or leave the 1 g weight: that's two choices.
You either use or leave the 5 g weight: that's two choices.
You either use or leave the 10 g weight: that's two choices.
You either use or leave the 20 g weight: that's two choices.

Each weight in your set is either used on the scale or left behind. If you have 4 weights, then the number of possibilities is 2 x 2 x 2 x 2 = 2⁴ = 16 - the same answer we got earlier. And you can also see how the general prediction agrees with the predictions from Pascal's triangle.

I hope this gives you a good start on your own explorations, Alyssa!
Stephen La Rocque>