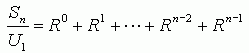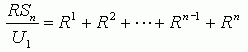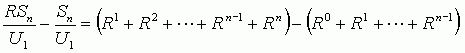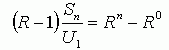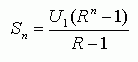Name: Andre, Parent of a secondary school student

In a particular geometric sequence, U₃=-3.6 and U₁₀=12.9. Find S₁₆ and S₁₇.

Hi Andre.

A geometric sequence is one where the ratios of successive terms are the same.

An easy example is { 1, 2, 4, 8, 16, 32, ...} where you can see that the ratio of each term to its neighbour is 2:1. Let's say we didn't know all these values, but we knew that the third element is 4 and the tenth element is 512. We want to figure out that constant ratio between terms and maybe a general expression for the nth term.

Each step, we multiply by the ratio, let's call that R. That means that there are 10-3 times that we are multiplying by R, so we relate the two known elements this way:

So solving for R, we get R equal to the seventh root of 128, which is 2. As well, we notice that if the third element is 4, then the first element is 4 divided by 2 twice, which is 1. Once we know the first element and the common ratio, we have the expression for determining any element in the sequence:

Where U_n is the nth element in the series, U₁ is the first element and R is the common ratio.

Your sequence is the same, but with different numbers.

Now I think when you refer to S₁₆ and S₁₇, you are referring to the sums of the sequence from elements 1 to 16 and 1 to 17, respectively. That is,

We should now expand this using our expression for U_n:

When we divide by U₁, we get:

This is just an equation. So we can do what we like to one side as long as we do the same to the other. Let's multiply both sides by the constant ratio R:

Now we'll do something quite clever: we'll subtract the last two equations! We can do this because we are subtracting equal quantities from both sides of the equal sign:

Notice now how all those intermediate terms disappear?

So we can now solve for S_n:

Hope this helps you!
Stephen La Rocque >