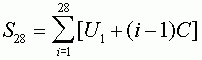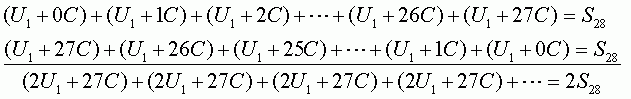From Angel, a post secondary student:

I am having trouble with these 2 problems and am really hoping you can help please as soon as possible.

a. In a particular arithmetic sequence, u6 = 344.5 and u20 = 88.3. Find S28 .
b. In a particular arithmetic series, S10 = 495 and S15 = 1005. Express S15 in sigma notation.

Hi Angel.

An arithmetic sequence is one where the difference between successive terms is a common difference (let's call it C). That is,

That means that when you compare U₂₀ to U₆, you get:

From this expression, you can figure out what C is. Then you can use the same idea in reverse to figure out the first term U₁:

Once you know the common difference and the first element in the arithmetic sequence, you can represent the sum of 28 terms as:

Which you can expand to:

This looks like a lot of adding to figure out, but look what happens if you write it out twice: once forward and once backward, then add the two equations:

You get all the same terms! Since there are 28 of them (from 0C to 27C), you can simplify this to:

Now you just have to solve for S, plug in the numbers you got for U₁ and C and you have your sum.

Now in part (b) of your question, you have two different sums and you have to express the second sum in sigma notation. You'll have to use the first two sums to find U₁ and C.

Let's look at the general form of the sum:

You can write out both of your sums S₁₀ and S₁₅ using 10 and 15 as the values of n. Then you have two equations with two unknowns (U₁ and C) that you can solve in the usual way. Once you have U₁ and C, you can substitute those into the form of the sigma notation I showed you earlier to finish your answer.

Hope this helps!
Sue