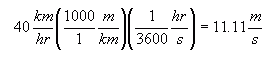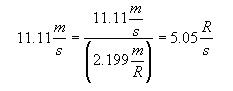Name: Ben
Who is asking: Student
Level of the question: Secondary

Question: How do you (a) express angular speed in terms of linear speed and (b) express linear speed in terms of angular speed?

Hi Ben.

Linear velocity is the distance travelled in a straight line per unit time. Angular velocity is the angle travelled per unit time.

By far the easiest example to see this is in Uniform Circular Motion. For example, a pebble embedded in your bike tire is travelling in uniform circular motion.

Let's say that your bike tire's outside diameter is 70 cm and you are moving at a peppy 40 km/hr. Remember that (ignoring skidding) the tire maintains traction with the road at all time, so the distance you travel, and the speed you travel is the same as the speed of the tire. If we convert that speed to meters per second, we get:

That's the bike speed, so that's the linear velocity of the bike. Since the bike and the tire are in constant contact, that's also the linear velocity of the pebble in the tire.

Angular velocity has to do with angles, as its name tells you. It is expressed in the form of what angle is rotated in a certain amount of time.

Angles can be measured in many ways: rotations, degrees, and radians. For example, a 10000 rpm hard drive refers to its angular velocity: 10000 rotations per minute. So how fast is our pebble moving rotationally?

That pebble, we know, moves the equivalent of 11.11 m/s linearly, but it is travelling around the circumference of the tire. If the tire's outside diameter, d, is 70 cm, then the circumference length is πd which is about 2.199 m.

If we divide the linear velocity by the circumference of the tire, we know how many rotations per second that tire (and therefore the pebble) is moving - angularly:

where R = rotations.

That's an angular velocity: how much it turns per unit time. If you want to convert this to degrees, you just multiply by the number of degrees per rotation (360), if you want to use radians instead, multiply by 2π radians per rotation.

Now let's try the other direction. Let's say you know an angular velocity and are trying to figure out the corresponding linear velocity. Hint: it's pretty fast!

Take as an example the earth's rotation. You know what its angular velocity is: how much it turns per unit time. Obviously that is one rotation per day!

Let's ask ourselves what the linear velocity is of a lock on the Panama Canal. That's close enough to the equator for us to use the diameter of the earth at the equator (12756 km) as our reference. What is the circumference of the earth at this point?

It you calculate the circumference, you can multiply that by the angular velocity and you get the linear velocity.

Here's something really interesting: Because the angular velocity depends on the circumference (and by implication, the radius), you can have something two things travelling at the same angular velocity, but different linear velocities.

Let's think of the (front) sprocket set on your bike. If you change from a small sprocket to a large sprocket, and keep your legs moving around the same number of rotations per minute (the same angular velocity), then you will go faster. That's because the linear velocity of the chain is what is driving the speed of the bike. So when you changed gears, you moved from a small radius sprocket (and therefore a small circumference) to a large radius (circumference) sprocket. When you multiply these two by the same angular velocity, you get a larger linear velocity with the large sprocket!

So large sprocket with twice the radius of a small sprocket should make you cover twice the distance in the same number of rotations of your legs.

To summarize:

• Divide the linear velocity by the circumference to get the angular velocity (in rotations per unit time, which you can then convert to whatever other unit you are interested in).
• Multiply the angular velocity (in rotations per unit time - convert first if you need to) by the circumference to get the linear velocity.

Hope this clears it up for you!
Stephen La Rocque>