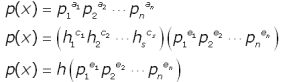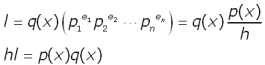Question from Bharath, a secondary school student:

The HCF and LCM of polynomials p(x) and q(x) are h and l respectively and p(x) + q(x) = h + l, show that
[p(x)]²  + [q(x)]² = h² + l²

Hi Bharath.

To aid our other readers, "HCF" = highest common factor (also known as greatest common divisor) and "LCM" = lowest common multiple. I am going to write as if p(x) and q(x) are integers, the argument when p(x) and q(x) are polynomials is similar.

Recall that each number can be uniquely represented by its prime factors.

Consider h and its expansion. It is the set of all the prime factors which p(x) and q(x) have in common, so all its terms are represented in the prime expansions of p(x) and q(x). We can write this by changing the exponents on the expansion of p(x):

Of course, some exponents e_i may be 0, that doesn't matter because those factors become 1.

For brevity, let's call that product of primes in the parentheses of the last equation above, S. We can now interpret S as representing all those primes which are not represented in the expansion of q(x) (otherwise they'd be in h as well).

This means that any common multiple of p(x) and q(x), of which l is the lowest, must divide the product of q(x) and S. In equation form, that is:

So the product of the HCF and the LCM of two numbers equal the product of the original numbers!

You can use this to complete the problem.

Hope this helps,
Stephen La Rocque.