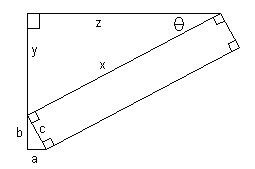
I'm currently designing a garage and came upon this interesting math problem. I've tried using various methods to solve it but have so far been unsuccessful. I've included a picture as its far easier to show you my question than explain it verbally. I realize it could be done by trial and error but i'm looking for a real solution.

I've redrawn the diagram and added some extra labels for the sides that will help us. Notice that although it wasn't explicit in your diagram, I have assumed that the rectangular-looking part is indeed a rectangle (all angles are right angles).

The first thing to notice is that the angle formed by sides c and b is congruent to theta. That means the two triangles are similar. Similar triangles have the property that the ratio of corresponding sides is equal. In our diagram, that means z/b = x/c.

From your measurements, we know that b = 36.5 - y and from the pythagorean theorem, we know that y = sqrt(x² - z²) and b = 36.5 - y. Let's substitute those into the ratios equation:

z/(36.5 - sqrt(x² - z²)) = x/c

If you put the values z = 118.75 and c = 0.5 into this equation, you get

118.75/(36.5 - sqrt(x² - 118.75²)) = x/0.05, or
36.5x - 118.75/2 = x sqrt(x² - 118.75²)

Squaring both sides and simplifying yields

x⁴ + 15433.8 x² - 4334.38 x + 3525.39 = 0

We used Mathematica to solve for x and got four solutions, only one of which makes sense for your situation. The solution is x = 124.09 feet.

Since the cosine of the angle theta is z/x we used the inverse cosine function to find that theta is 0.2945 radians or 16.87 degrees.

Stephen and Penny