Question: My daughter is working on a math project & we are having a hard time finding the volume & surface area of a rectangular pyramid. Can you help us with this? Thank you very much.

Hi Cheryl,

The volume of a pyramid is

 ¹/₃  (area of the base) (height)

I don't know a nice way to prove this without using calculus. You can see what I did for a particular situation in the answer given to Becky who asked a similar question.

For the surface area I am going to assume that the base is a rectangle (not necessarily a square) and the apex of the pyramid P is directly above the centre of the base.

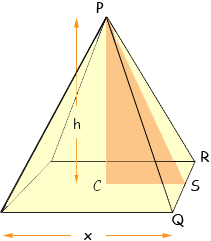
The surface area is the area of the rectangular base (length width) plus the areas of each of the four triangular faces. The area of a triangle is ¹/₂ base  height so all that remains is to find the height of each of the triangular faces. I am going to show you how to find he height of the triangular face PQR in the diagram.

In the diagram C is the centre of the rectangular base of the pyramid, S is the centre of the side QR of the base, h is the height of the pyramid and x is the length of the side of the base as shown. Thus the triangle PCS is a right triangle with side lengths h and ^x/₂. Thus you can use Pythagoras theorem to find the length of the hypotenuse PS which is the height of the triangle PQS. Use this height to find the area of the face PQR.

Repeat this process for the other three triangular faces. Actually they come in pairs so you only need to do this calculation twice, or if the base is a square all four triangular faces have the same area.

I hope this helps,
Penny