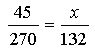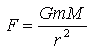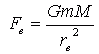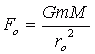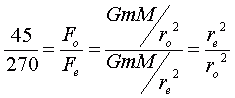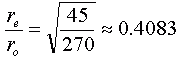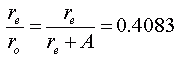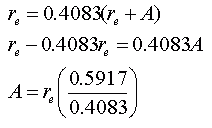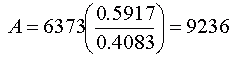|
 |
|
From: Chloe, a middle-school student If a person who weighs 270 pounds on Earth weighs 45 pounds in space, how much would a person weigh in space who weighs 132 pounds on Earth?
|
|||
|
Hi Chloe. In space, things don't really "weigh" much at all - far less than your question suggests. In fact, generally, we don't think of things as weighing anything in space, because weight is a measurement of the force of gravity on an object. When you are away from massive objects like the Earth, you don't experience much gravitational attraction towards them. Nevertheless, the figures you are describing could actually happen in a particular Earth orbit (9236 km or 5740 miles). Let's say that is the point in space you are talking about. The important point to recognize here is that the weight fractions are the same. That is to say that if we let the variable x represent the weight of the second person in low orbit, then:
You can see that the fractions are the same. So you have to find the value of x that works here. Re-arrange the equation to solve for x and you'll get your answer. Hope this helps, PS: If you are interested in how I figured out the orbital altitude 9236 km, here is how I did it. The math might be a bit more advanced than you are doing in class, but it's really just algebra with lots of variables. There is a special equation in science that is used to calculate the gravitational force between any two objects. Here it is:
In this equation, F is the force of gravity (the weight), G is a special universal gravitational constant (whose value doesn't matter for our discussion), m and M are the masses of the two objects (the person and the Earth) and r is the radius from the center of the person to the center of the Earth. The masses of the person and the Earth don't change, but the location - the radius between them - changes and so does the weight. So there are really two of these equations, one for the person on earth and one for the person at this location in orbit. Let's replace the F with Fe and Fo (for earth and orbit) and r with re and ro . If you haven't used variables like these before, don't worry - they don't mean anything different than if we used x, it's just easier to use variables whose name reminds us of what they represent:
Now you remember what I indicated earlier in your question: the fractions are the same. The "weight" in orbit divided by the weight on Earth is the same no matter how much the person weighs. Fo is the weight in orbit and Fe is the weight in orbit. So if we write the fraction we know using the first person's weights, then we can write in the fraction using our variable names and the equations they represent. Then we'll simplify that:
Do you follow all that? First I showed you the fractions were the same. Then I replaced Fo and Fe with the equations for each of them. Then I cancelled out terms on the top and the bottom of the fraction. If you understand this, then you will see that the mass of the Earth and the mass of the person don't matter at all! We can simplify this. I'll use a calculator and figure out the square root here:
Now let's think a bit about ro - it's the radius from the center of the Earth to the center of the person in orbit. But that distance is the same as the radius of the Earth (re ) plus the altitude of the orbit above the surface of the Earth. So let's now define A as the altitude. Then,
So let's substitute this into our last equation:
Now we need to solve for the variable A, the altitude we need to find:
Now we need to actually look up what is re, the radius of the earth. According to my reference book, the radius of the Earth is about 6373 km. So let's put that number in place of re in this last equation and we'll have the altitude:
That's the altitude above ground in kilometers. In miles, you'd divide this by 1.609 because that's how many kilometers there are in a mile. Hope you found this interesting! Stephen La Rocque > Hi Chloe, My reaction to reading this question was quite different than Sue's. I saw that the second person weighs slightly less than half of the first person on Earth so she will weigh slightly less than half of the first person in space. Half of 45 pounds is 22.5 pounds so she will weigh 21 or 22 pounds in space. In many situations this number sense answer is sufficient. Penny |
|||
 |
 |
 |