|
 |
|
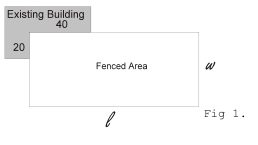
I hope you can help me out with the attached problem, It has been driving me crazy.
|
||||||||||||||
Hi Daryl. I think I can at least answer the first part of your question. You are trying to find a way to maximize the area of your enclosure, so the first thing you need to find is the shape. The method that leaps immediately to mind is the one in your diagram - a rectangular pen. The area of a rectangle is A = L x W. The perimeter of a rectangle is 2L + 2W. If we use the building to extend our perimeter fence, then the total perimeter your fencing can enclose is 40 + 20 + 100 = 160 linear feet. That means we can solve for width: 160 = 2L + 2W W = 80 - L Using that to express the Area A, At this point, you can try to find the maximum using the derivative of this expression to find a zero slope: So setting this derivative to zero, L is 40. That means when L = 40, the area of your rectangular pen is maximized. Since W = 80 - L, then the width is also 40. Here's a picture that shows a 40 x 40 foot enclosure (1600 sq ft.) using the 100 ft of fencing: 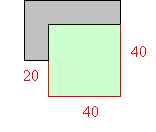
That's the straightforward approach, but does a rectangular shape give the greatest area? Without getting into the proof in detail, consider that if we had 160 ft of fencing (and no building), our largest area rectangle would be as shown above, but if we draw a circle whose circumference, C is 160 ft, then the radius is
and the area is That's significantly more than the 1600 sq. ft. we got using a rectangular (square) approach. We'd like to use this idea for our problem but we don't really have a full circle. Still, we can use the fencing to form a circular lobe, something like this: 
We know the arc length is 100 ft. - that's how much fencing we have. But at this point we haven't really determined exactly what area the new enclosure is. So let's redraw our diagram with some extra reference lines and points and angles labelled: 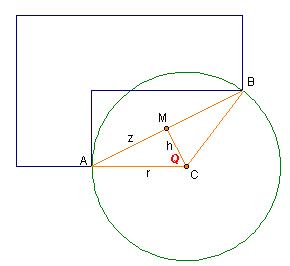
Now the enclosure is composed of three pieces: 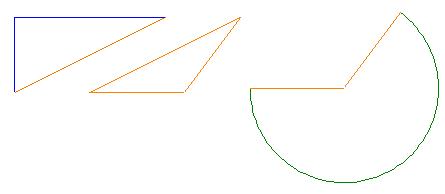
The first triangle's area is simply half the base times the height: 1/2 x 40 x 20 = 400 sq. ft. So that's done. The second triangle's area can be found if we know the lengths of all the sides. Heron's formula says its area is where a,b,c are the lengths of the sides and s is half the perimeter (a+b+c). In our case, we know that the long side is the hypotenuse of the first triangle, so using the Pythagorean Theorem, it works out to: 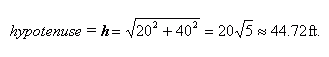
The other two sides of the triangle are each the radius of the circle, which we don't know yet. The area of the circular shape depends on the radius and the subtended angle, neither of which we know yet, but we do know the length of the arc. It is the amount of fencing: 100 ft. Remember that if you work in radians instead of angles, the arc length is just the angle times the radius. So if the wide angle is called β, then 100 = βr or r = 100/β. Let's go back to the second triangle. In the earlier diagram, we subdivided it further. Notice that it must be isosceles because two of its sides are the same (r). That means we can bisect the other side with a perpendicular that goes through the point joining the equal sides. Here is that subdivided triangle again: 
Because we bisected AB, it's easy to see that triangle AMC is congruent to triangle BMC, so if we solve one, we solve the other. Let's look at AMC closely. We know the length of AM - it is half the hypotenuse of the first triangle, h: (we've labelled this z on our diagram). The line from M to C is perpendicular to AM, so that is a right angle at M. That means that the sine of angle Q is z/r. We know z, but still have two unknowns here. Let's solve for r: But we can quickly observe that the earlier angle β added to two Qs gives the full circle. That means that β = 2π - 2Q. That makes Ah! Now we have two equations for r, we can solve for Q! At this point, I'm going to cheat a bit. Even though there is just one variable in this equation, it's a bit tricky to solve it exactly and for fencing, an approximation will do. (Side note: Harley explains this in a quandary from Amandeep here.) We do know that 0 < Q < π. If you try some values of Q, you can pretty quickly zero in on a good approximation of Q = 1.12452 radians. Now that we know Q, we can solve for the radius r:
And knowing the radius, we know all three lengths of that triangle ABC, so we'll figure out the semi-perimeter and then use Heron's formula to calculate its area:
Also, knowing the radius lets us calculate β because if r = 100/β, then
Now armed with the radius r and the angle β, we can calculate the area of the circular region by multiplying the area of the full circle by the ratio of β to the angle of the full circle (in radians, that is 2π of course):
Now we have all three areas. Their sum is:
Hi Daryl, The wording of the second problem is strange. I think you want to minimize the fence material to minimize the cost. I am going to assume also that you want a rectangular pen. If this is so then the area of the pen is 1800 square feet and hence
The length of fencing, which I am going to call F is given by
Use the area formula above to write F as a function of one variable and then use calculus as Sue did to minimize the amount of fencing material. Penny |
||||||||||||||
 |
 |
 |