My name is Andrea and my son, Doug, and I were wondering what the capacity of our hexagon fish tank was but it’s been so long since I’ve been to school that I’ve forgotten the formula to do so. Would you please help us? The dimensions are: 27 ¾ W x 24L x 29H or one side (glass panel) is 14W x 29H.
Thank you,
Doug and Andrea

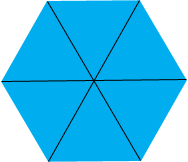
Hi Doug and Andrea,

I am assuming the measurements are in inches.

The volume of your tank is the area of the base times the height. Since the base of your tank is a hexagon you need to find the area of a hexagon. To do this draw a hexagon and join the opposite vertices to divide the hexagon into 6 congruent triangles. Thus the area of the hexagon is 6 times the area of one of the triangles.

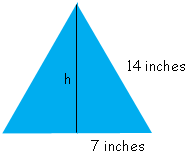
The sum of the 6 angles at the centre of the hexagon is 360^o and hence each of the 6 angles measures 60^o. By the symmetry, each of the other angles of the triangles measure 60^o and hence each is an equilateral triangle with sides of length 14 inches. Look at the bottom triangle.

Draw a perpendicular from the apex to the base and call its length h inches. You then have a right triangle with sides of length h, t and 14 inches and thus, using Pythagoras theorem,

h² + 7² = 14²

and thus

h² = 14² - 7² which gives h = 7 √3 inches which is approximately 12.12 inches

The area of a triangle is (half the base) height and hence the area of each of the 6 triangles that make up the hexagon is

7 7 √3 = 84.87 square inches.

Thus the area of the hexagon is

6 7 7 √3 which is 509.22 square inches.

Finally the volume of the tank is

(area pf the base) height = 6 7 7 √3 29 = 14767.5 cubic inches.

There are 231 cubic inches in an American gallon and thus the volume of the tank can also be expressed as

 ^14767.5/₂₃₁ = 64 gallons

Penny