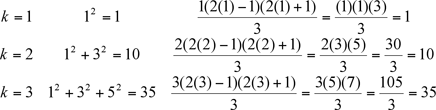Question: 1)by mathematical induction prove that 1² + 3² + 5² + ...... + (2k-1)² = (1/3)k(2k-1)(2k+1) for all positive integers k.

2)show that the contrapositive of the following statement is true. if 1 + M⁷ is even, then M is odd.

Hi Eben.

I can maybe help with your second problem.

Given a statement in the form

"if (A) then (B)",

the contrapositive is formed as

"if (not B) then (not A)."

So in your statement, "1 + M⁷ is even" represents A and "M is odd" represents B.
That makes the contrapositive of your statement:
"If M is even, then 1 + M⁷ is odd."

Can you show why this is true?

Problem 1.

Let’s use a formal proof approach to this question.

Theorem:

for each positive integer k

Proof:

Let’s start by looking at a few small values for k and see if both sides of the equation give the same results:

(For the proof by induction you only need to check the case when k = 1 but I like to check a few cases just to see if the expression seems to be correct.)

These all work, but what about ALL the larger values of k?  Let’s assume that it does work for all the values of k up to and including p (which we just demonstrated is indeed true for p up to 3).  That is,

for k = 1, 2, ··· , p

In particular, we are assuming that

We want to show that if the statement above is true, then the next possible p (which is p+1) is also true.  That is, can we show that

equals

If it is, this argument applies to the next p, and the next – in other words, for all larger values of p (completing the proof).

Can you complete the proof by showing Z = ?

Stephen La Rocque>