I am an education student in a class that teaches us how understand how math works well enough to be able to teach it when it comes up in our context area(not math). We had a question on volume.

A box factory has a large stack of unused rectangular cardboard sheets with the dimensions of 26 cm length and 20 cm width.
The question was to figure what size squares to remove from each corner to create the box with the largest volume.
I began by using a piece of graph paper and taking squares out. I knew that the formula L X W X H would give me volume. After trial and error of trying different sizes I found that a 4cm X 4cm square was the largest amount you can take out to get the largest volume. My question for you is two parts

First: Why does L X H X W work? And second, is their a formula that one could use, knowing the length and width of a piece of any material to find out what the largest possible volume it can hold is without just trying a bunch of different numbers until you get it. If there is, can you explain how and why it works.

Thank you. This is not the answer I need for class, already have that, I just became curious.

Elizabeth

 

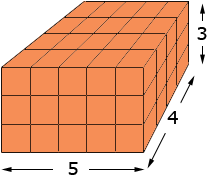
Hi Elizabeth,

Imagine that you have a box that is 5 centimeters long, 4 centimeters wide and 3 centimeters high. I want to completely fill it with cubes that are 1 centimeter in each dimension. I can start by placing 4 row of 5 cubes each on the bottom of the box using 4 5 = 20 blocks.

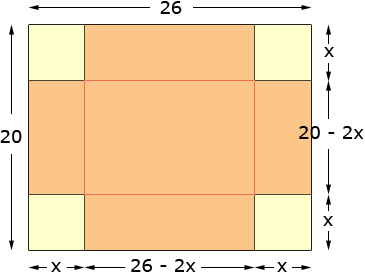
I can add two more layers since the box is 3 centimeters high, and hence I use
20 3 = 60 cubes. Since I have completely filled the box its volume is 4 5 3 = 60 cubic centimeters. This idea is the reason that the volume of a box, L cm by W cm by H cm is L W H cm3.

Your second question about forming the largest volume box possible involves a use of calculus. Let's look at your 26 cm by 20 cm rectangle and imagine that we cut out corners as you described, and then formed a box. I want to see what happens for various sized square cut-outs so I am not going to use a specific size for the cut-outs, rather I will say that the cut-out is x cm by x cm.

As you can see in the diagram, when you cut out the corners and fold up the sides to make a box its dimensions are 26 - 2x cm long, 20 - 2x cm wide and x cm high. Thus its volume is

(26 - 2x) (20 - 2x) x cm3.

I want to call this expression V(x), V for volume and x for the sides of the square removed. Thus, simplifying I get

V(x) = 4 (x3 - 23 x2 + 130 x) cm3.

This is the expression you calculated in your experiments (probably not in this form). What you found was that when x was small (1 cm) the volume was quite small and the volume increased for x = 2 cm then 3 cm and 4 cm, but when x became 5 cm the volume started to decrease. What I want to do is find the exact value of x where this change from increasing to decreasing occurs. This is where calculus enters the process.

A function called the derivative of V(x) (designated V'(x)) measures the rate at which V(x) changes as x changes. V'(x) is positive for small values of x (the volume is increasing as x changes from 1 to 2 etc.) and V'(x) is negative for larger values of x (the volume is decreasing as x changes from 4 to 5 etc.) I want to find where V'(x) is zero, that is where it changes from being positive to being negative.

Using calculus I find that

V'(x) = 4 (3 x2 - 46 x + 130)

so I want to solve

4 (3 x2 - 46 x + 130) = 0

I solved this with the general quadratic and found x = 11.58 cm and x = 3.74 cm. If you look back at the diagram you will see that x = 11.58 cm is impossible, so this answer of the mathematical problem is not a valid answer to the physical problem of cutting out square corners. The answer I am looking for is x = 3.74 cm.

Why did you get x = 4 cm and I got x = 3.74 cm? My technique allows for fractions and I expect that you only used integers. If you go back to your calculations and find the volume when you remove a 3.74cm 3.74cm square you will obtain a slightly larger value then when you removed a 4cm 4cm square.

Penny