 |
 |
|
From: Emilio Hi, I need to find the measure of the sides of the hexagon that the area is 58 square units.
|
|
Hi Emilio. I'm going to assume that your question is about a regular hexagon (a hexagon where all the sides and the angles are the same). Here's a diagram to help us:
Can you see from symmetry that there have to be eleven other triangles in the hexagon that are congruent to the one I've drawn? That's because the segment a is what is called the apothem - it is a perpendicular bisector of the side and ends at the center. The area of the triangle I've drawn is ½ab, of course, so the total area of the hexagon is twelve times that: 6ab. If we say that the total area is A, then A = 6ab. We need to solve for 2b, so that would be 2b = A / 3a. But what is a? Since this is a right-triangle, let's use the angle β to help us: tan β = a / b, so a = b tan β. If we substitute that into our earlier expression, 2b = A / 3(b tan β). Since you are given A (58 square units) and can easily determine β for this shape, you can solve for b now. Hope this helps,
|
 |
 |
 |
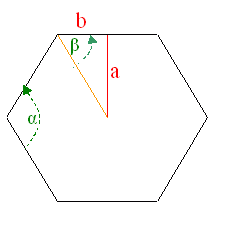 You should be able to figure out the angles
You should be able to figure out the angles