|
 |
|
Hello,
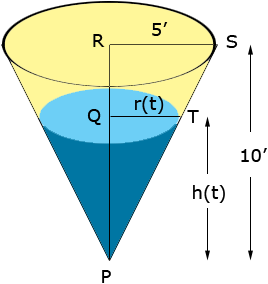
My name is Erin and I am a senior in high school. I have a problem from my calculus class and am having trouble getting started. We are working with Related Rates. The problem is as follows... Water runs into a conical tank at the rate of 9ft3/min. The tank stands point down and has a height of 10 ft. and a base radius of 5 ft. How fast is the water level rising when the water is 6 ft. deep? (V=1/3 pi r2 h). Any help would be greatly appreciated!
|
|
Hi Erin, You have V=1/3 pi r2 h but let's be more explicit. Let V(t) be the volume of water in the tank at time t minutes, h(t) be the height of the water at that time and r(t) the radius of the top of the water at time t. You want to find the rate at which the height of the water , h(t), is changing at a particular time, the time when the height of the water is 6 ft. The rate you want, the rate at which h(t) is changing is h'(t). You do know one rate, V'(t) = 9 cubic feet per minute at every time t. You can find a relationship between V'(t) and h'(t) by differentiating both sides of
with respect to t but, unfortunately the right side will contain not only h'(t) but also r'(t). Somehow you need to eliminate the r(t) factor from the right side of
to make this procedure work. The geometry of the situation gives you the information you need.
From the diagram triangles SRP and TQP are similar and hence
Thus
and hence r(t) = 1/2 h(t). Substitute this into the expression V(t)=1/3 pi r2(t) h(t) and then differentiate both sides with respect to t. Penny |
 |
 |
 |