From: Geecee

At a local village gala, the entire population turned up, 500 people. The event raised £3,000. Tickets were priced as follows: £7.48 men, £7.12 women and £0.45 children.
How many children were there?

Hi Geecee.

First let's look at how the people add up. Let's use m, w and c to represent the number of men, women and children:

Now let's write out the receipts (converting things to whole numbers by multiplying first by 100):

Substitute in our earlier evaluation of m and then simplify:

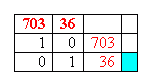
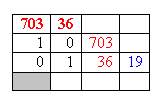
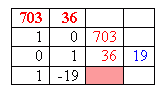
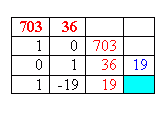
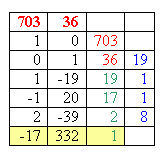
Now there are some important facts about this last expression: w and c are both whole numbers and are between 0 and 500. What fits? For this, we'll use the Euclidean Algorithm. The Euclidean Algorithm will help us find w and c. We already can see that 36 and 703 are relatively prime, so we know the GCD is 1, but if we use the Euclidean Algorithm, we'll be able to see a general form for all the integers that fit into 74 000 = 36w + 703c.

Here's a neat notation method for using the Euclidean Algorithm. One of our experts here at Math Central (Penny) taught it to me and I thought I'd pass it along to you. The method just keeps track of things neatly and quickly.

The way it works is as follows:

You start by writing your two initial numbers in the spots that are in red and writing those 1's and 0's in the first two rows. The next step is to figure out what goes in the fourth column (blue area). How many times does the number to its left (36) go into the number above it (703)? The answer is 19. Write that in. This column will store the multiplier for the row. We use it in the next step.

The next step is to figure out what goes in the grey area. To get this, take the value two squares above it and subtract the value below it times the blue number in the row above. In this case, 1 - 0(19) = 1. The second column is done the same way: 0 - 1(19) = -19.

The red box works the same as well. Starting with the value two squares up, subtract the square above times the blue number. In this case, 703 - 36(19) = 19.

Now we just repeat this process for row after row until the value in the third column is 1 (actually we are stopping one row before it is zero, sometimes the third column goes to zero whilst bypassing 1).

Here's the completed table with the important results highlighted in yellow. It is telling us that 703(-17) + 36(332) = 1.

We are really interested in 703c + 36w = 74 000, so let's multiply by 74 000:

So far, these numbers look enormous! But don't give up yet - obviously the number of women isn't -1 258 000. But we can create a general form for this equation.

What happens if we choose some arbitrary integer k and add 36k to the first set of parentheses? We've added (703)(36)k to one side of the equation, so we either need to add it to the other side or subtract it again. Let's subtract it again by putting -703k into the second set of parentheses:

This works for any integer value of k! What we want to find is a k that gives us a suitable w and c.

Let's summarize what we know:

So then c = 36k - 1 258 000 and w = 24 568 000 - 703k for some special value of k. Let's use w's domain restriction to determine k:

But since k is an integer, there is only one possible value for k: 34 947.

Now that we know k, we can solve for c: 36k - 1 258 000 = 36(34 947) - 1 258 000 = 92. This is certainly between 0 and 500. So we have an answer.

To check our answer, let's calculate the number of men and women and make sure everything is right.

Both of these numbers are also between 0 and 500. For the final step in our check, let's put these numbers into the receipts and see if we get £3 000:

Stephen La Rocque.>