Question: The last digit of a six-digit number is 2. If the 2 is moved to the start of the number, the new six-digit number is only a third of the original number. Find the original number.

GG,

I have three responss to your question.

From Penny

Look at the problem this way. You have a five digit number that you make into a six digit number in two different ways, by appending a 2 at each end of the number. Suppose that F is the five digit number. To place a 2 in the units position first multiply F by 10 to put a zero in the units place, and then add 2. Thus one of the two numbers is

10F + 2

To put a 2 at the start of the number you can add 200000 to F. Thus the second of the two numbers is

200000 + F

Can you complete the problem now?
Penny

From Chris

You can easily guess the answer by knowing what the decimal expansion of 1/7 looks like. But there is a really neat way to solve this kind of puzzle. Think of your number as being the repeating block of a repeating decimal:

x = .abcde2abcde2...

Your problem says that if we define y to be the repeating decimal

y = .2abcde2abcde2...,

then these two rational numbers satisfy the equation,

x = 10y - 2 = 3y.

now solve the right-hand equation for y and use that solution to find your desired number x.

Chris

and from Paul

Let the original number be ABCDE2, where A, B, C, D and E are digits.
And the given information means:
2ABCDE
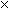3
-------------
ABCDE2

Consider 3 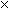E
This must produce a number whose one's digit is 2, which only works
when E = 4 (3 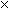4 = 12).

We now have:
2ABCD4
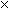3
-------------
ABCD42

Consider 3 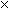D
3 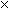E = 12 so we must carry the 1, so 3 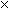D + 1 must produce a number
whose one's digit is 4, which only works when D = 1 (3 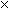1 + 1 = 4).
Note there is no carry to the next column.

We now have:
2ABC14
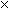3
-------------
ABC142

3 x C must produce a number whose one's digit is 1, which only works
when C = 7 (3 x 7 = 21). Note that we must carry the 2.

We now have:
2AB714
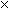3
-------------
AB7142

3 x B + 2 must produce a number whose one's digit is 7, which only
works when B = 5 (3 x 5 + 2 = 17). Note that we must carry the 1.

We now have:
2A5714
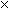3
-------------
A57142

3 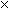A + 1 must produce a number whose one's digit is 5, which only
works when A = 8 (3 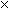8 + 1 = 25). Note that we must carry the 2.

We now have:
285714
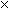3
-------------
857142
Note that this calculation works.
Therefore, the original number is 857142.

Paul