Question from Glenn:

Given the diameter of the sphere 10cm. find the largest cube inscribe in the sphere.

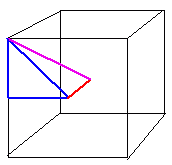
Hi Glenn.

Let's first do a bit of reasoning. The largest cube you can inscribe in a sphere is, of course, the one where all the corners of the cube touch the sphere. That's easy to visualize, but how does it help?

Think about where the center of the sphere and the center of the cube have to be: in the same place. That means that the distance from the center of the cube to a corner of the cube has to equal the radius of the sphere.

So now you need to consider how to find the length of the side of a cube when you know the distance from the center to the corner. I'll draw a picture and you can figure out the ratios involved by using the right triangles:

Hope this helps,

Stephen La Rocque.>