Problem: Carol was traveling from Asheville, North Carolina, to Indianapolis, Indiana, by bus. At the halfway point of her trip, in terms of distance, she fell asleep. When she awoke, her distance to Indianapolis was half the distance that she had traveled while she slept. For what fraction of her trip did Carol sleep?

Thanks!

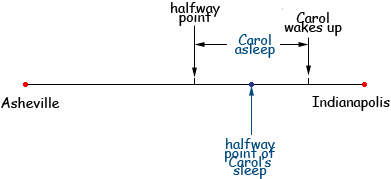
We have two quite different responses to your question, one from Penny and another from Stephen La Rocque.

Hi Grace,

I drew a diagram of the road from Asheville to Indianapolis.

I marked the halfway point of the road (where Carol fell asleep) and the point where she awoke. The distance from this point to Indianapolis is half the distance from where she fell asleep to where she awoke. I put a blue dot at the point which is halfway through her sleep. Thus for the second half of her trip I have divided the road into three equal parts. For two of these parts she was asleep. For what fraction of the entire length of the road was Carol asleep?

Penny

Hi Grace.

This is a problem that algebra can solve. There aren't any numbers in this problem, so we'll use variables to represent the quantities and try to change this into mathematical form.

"Carol was trveling from Asheville, North Carolina, to Indianapolis, Indiana, by bus."

Okay, let's call the total distance of the trip T.
"At the halfway point of her trip, in terms of distance, she fell asleep."

We can say she fell asleep at T/2.

"When she awoke, her distance to Indianapolis was half the distance that she had
traveled while she slept."

She slept for a distance. Let's call that S. When she awoke, there was a remaining
distance to go before she reached the destination, let's call that R.

So the total distance (T) is the Remaining distance (R) plus the distance she was
asleep (S) plus the first half of the trip when she was awake (T/2). That means:

T = R + S + T/2

But that last quote also tells us that R = S/2. So that means:

T = S/2 + S + T/2.

The question is "For what fraction of her trip did Carol sleep?". That's asking for
the fraction S/T. Can you re-arrange the equation above into the form S/T on one
side and a numeric value on the other?

Hope this helps!
Stephen La Rocque>