|
 |
|
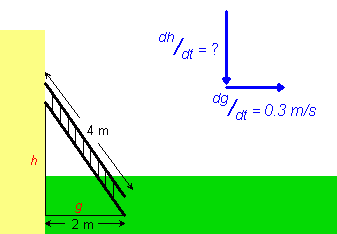
From: Harsh, a secondary school student I need to use calculus to solve this problem: A ladder 4 m long rests against a vertical wall. If the bottom of the ladder slides away from the wall at a speed of 30 cm/s, how quickly is the top of the ladder sliding down the wall when the bottom of the ladder is 2 m from the wall? Thanks.
|
|
Hi Harsh. Here's a diagram that shows what is happening here: For a particular instant in time, you are given the speed of g (that is,dg /dt) and the distance g and asked to find the speed of h (that is,dh /dt). You need to start by creating a time-independent expression for h in terms of g. This is just the Pythagorean Theorem (ignore the 2 m measurement - it only applies at a particular time, but you can use the 4 m measurement since the ladder length is constant with respect to time). Now you differentiate both sides of the equation with respect to time. You'll need to use the chain rule twice. This gives you dh /dt on one side of the equation, which is what you want to find, and an algebraic expression on the other side which has dg /dt in it. The last step is to substitute in the values of dg /dt and g that you are given for this instant in time and you'll have your numerical answer. Watch your signs carefully because h is shrinking and g is growing, so you'll need to interpret your signs appropriately! Hope this helps,
|
 |
 |
 |