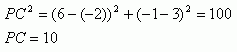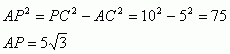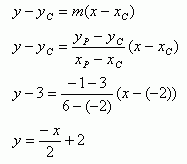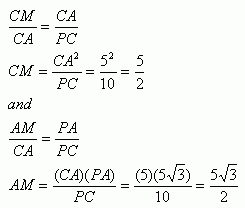|
 |
|
I have problems finding the point of tangency between the circle C
and the tangential line that passes through the point P (6, -1). I don`t know if it helps, but the center of C is(-2, 3) and its radius is 5.
|
|
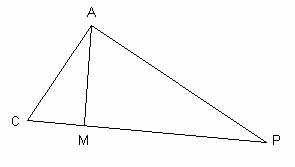
Hi Izumi. I double-checked your calculation for the center and radius and I agree. Let's start with a sketch so we can understand what is happening:
I've also drawn radii AC and BC. A tangent line on a circle is always perpendicular to its radius at the point of tangency, so
You know the radius AC is 5 units and that C is at (-2, 3) and P is at (6, -1). This is enough information to determine the length AP. Let's use the distance formula to calculate the length of PC:
Now we can use the Pythagorean Formula to find the length AP:
We are also going to need the equation of the line PC and since we have two points on the line (P and C) we can readily find the equation of the line:
Now we have a right triangle that we'll subdivide with a perpendicular from A down to PC, meeting it at point M.:
Remember that
Now with the location of C, the equation for the line PC and the distance CM, we can determine the location of M. I'll leave that to you. Once you have the location of point M, you need the slope of AM. Note that by symmetry, this must be the same as line MB, in other words, the line connecting A to B includes point M). Remember that AM is perpendicular to PC, so if PC's slope is -1/2 (and it is, that's what we calculated earlier) then MA's slope must be the negative reciprocal of that: 2. Finally, you have the point M and the slope for MA and the distance MA, so you can use this to find the actual location of A. By symmetry, point B is just the other direction along AB from M. You should work out the exact values (with square roots), but point A is roughly (2.2,5.8). Hope this helps,
|
 |
 |
 |
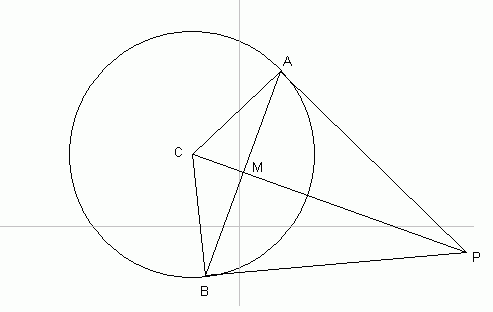 I called the center of the circle the point C and you can see by symmetry that there are actually two points (labelled A and B) which satisfy the conditions, because line AP is tangent to the circle and passes through P and so does BP, also tangent to the circle. So we are expecting two solutions.
I called the center of the circle the point C and you can see by symmetry that there are actually two points (labelled A and B) which satisfy the conditions, because line AP is tangent to the circle and passes through P and so does BP, also tangent to the circle. So we are expecting two solutions.