From: Jade, a secondary school student

Given: circle O = circle P, OP = 6 in this picture:

Find the area of the shaded region.

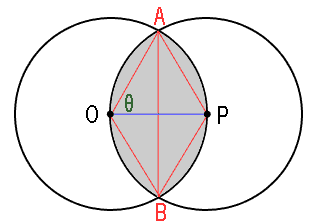
Hi Jade.

In a followup email, you indicated that O and P are indeed the centers of those circles and the shaded region is the overlapping area. I've re-drawn your diagram with some extra helper lines and some points labelled A and B:

Here's how to tackle this one, Jade. We're going to find the area of the APB arc region, that is, the shape that looks like this:

You can see that this shape is part of the sector AOB of the circle. If we can find the size of AOB, then the sector is just a ratio of that angle to the angle of a full circle (360 in degrees). So now we have to find the size of AOB. The way I've drawn it, you should see by symmetry that this angle is just 2Θ. So what's Θ?

Notice that P is a point on the circumference of circle O. This means that OP is the radius of circle O. You've said that the line segment OP is 6 units, so we know that the blue line in the diagram has length 6. But all radii of a circle are the same, so the radius from O to A is also 6 units. And the two circles are identical, so the segment from A to P is also 6 units. That means that AOP is an equilateral triangle, and you know the size of the angles in an equilateral triangle are all 60°, so that means Θ = 60°.

Now we know AOB = 2(60°) = 120°. Since a full circle is 360°, this is a third of the circle. That means the area of sector AOB is one third the area of the whole circle. We still need to remove that triangular part of the sector in order to get our APB arc region area though. That's the next step.

It should be clear that due to symmetry, AB is a perpendicular bisector of OP. That means those smaller triangles are all right triangles and the short sides are half the size of the hypotenuses (which are radii). So you know two sides of a right triangle, it is easy to use Pythagorus to solve the other leg.

You can see that two of these right triangles add together to make the triangular area we want to deduct from the area of the sector, so subtract twice the area of a small triangle from the sector area you got earlier.

Now you have the area of the shape, so just double it for your final answer!

Hope this helps!
Stephen La Rocque.