|
Hi Jade.
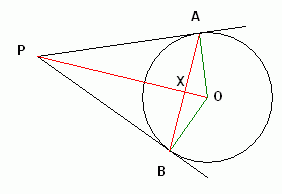
I've drawn a diagram and labelled some extra points and lines to help us.
1.  PAO is a right angle. This is because line segment AP is tangent to the circle. Tangent lines are always perpendicular to the radius (in this case, the radius is segment AO). Due to symmetry, the same goes for PAO is a right angle. This is because line segment AP is tangent to the circle. Tangent lines are always perpendicular to the radius (in this case, the radius is segment AO). Due to symmetry, the same goes for  PBO. PBO.
2.  PAO is congruent to PAO is congruent to  PBO. This is because they are two right triangles and two sides are congruent (AO is congruent to BO because both are radii and PO is congruent to itself of course). PBO. This is because they are two right triangles and two sides are congruent (AO is congruent to BO because both are radii and PO is congruent to itself of course).
3.  APO is congruent to APO is congruent to  BPO and AP = BP. Corresponding parts of congruent triangles are congruent (CPCTC). BPO and AP = BP. Corresponding parts of congruent triangles are congruent (CPCTC).
4.  APX is congruent to APX is congruent to 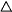 BPX. This is because of Side-Angle-Side (S.A.S.): AP, BPX. This is because of Side-Angle-Side (S.A.S.): AP,  APX, & PX are congruent to BP, APX, & PX are congruent to BP,  BPX, & PX. BPX, & PX.
5. AX is congruent to BX. Reason: CPCTC. This means PO is bisecting AB.
6.  AXP is congruent to AXP is congruent to  BXP. Reason: CPCTC. And since these are supplementary angles, they add up to 180 degrees. This means both of these angles are right angles. So PO is the right bisector of AB. BXP. Reason: CPCTC. And since these are supplementary angles, they add up to 180 degrees. This means both of these angles are right angles. So PO is the right bisector of AB.
7.  OAX is the complementary angle of OAX is the complementary angle of  AOX. This is because AOX. This is because 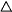 AOX is a right triangle. AOX is a right triangle.
8.  APO is the complementary angle of APO is the complementary angle of  AOP (which is also called AOP (which is also called  AOX). This is because AOX). This is because 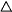 APO is a right triangle. APO is a right triangle.
9.  APO is congruent to APO is congruent to
 OAX. Because two angles complementary to a third angle are congruent. OAX. Because two angles complementary to a third angle are congruent.
10.  APB is twice the size of APB is twice the size of  OAB. This is because OAB. This is because  APB = APB =  APO + APO +  BPO (that's how it's composed) and BPO (that's how it's composed) and  APO is congruent to APO is congruent to  BPO due to CPCTC. BPO due to CPCTC.
Hope this helps!
Stephen La Rocque.
|






 PAO is a right angle. This is because line segment AP is tangent to the circle. Tangent lines are always perpendicular to the radius (in this case, the radius is segment AO). Due to symmetry, the same goes for
PAO is a right angle. This is because line segment AP is tangent to the circle. Tangent lines are always perpendicular to the radius (in this case, the radius is segment AO). Due to symmetry, the same goes for 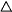 PAO is congruent to
PAO is congruent to