 |
 |
| Name: Jessica Who is asking: Student Level of the question: All Question: How do you work out an algebraic equation for the IQ of an isosceles triangle. I can do algebraic equations for regular shapes but am having trouble with this please could you help. Thank-you
|
|
Hi Jessica, If you have a simple closed curve with perimeter p units and enclosing an area A square units then the isoperimetric quotient of this curve is
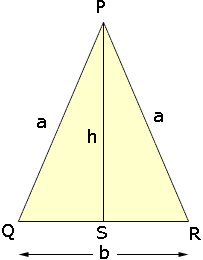
Suppose that the curve is an isosceles triangle with side lengths a, a and b as in the diagram below.
The perimeter of this triangle is p = 2a + b and the area is A = b/2 Penny |
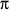A /p2 
h. The triangle PSR is a right triangle with hypotenuse of length a and sides of length h and b/2 . Use Pythagoras to express h in terms of a and b and substitute into the expression for A. Finally substitute these values for p and A into the expression for the isoperimetric quotient. |
 |
 |