Jim
10-12
other

In case the pic doesn't work:
Right angle triangle with a hypotenuse of 20 units.
Square inside the triangle with sides of 4 units, the square shares two sides with both legs of the triangle, and the corner touches the hypotenuse limiting the triangles size.

 

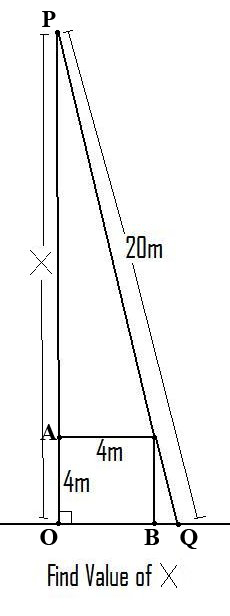
Hi Jim.

I labeled some points on your diagram.

Unfortunately I don't have a nice solution to your problem. Here is one solution.

Let y = |PA| and x = |BQ| then using similar triangles

y/4 = 4/x or x = 16/y

Also triangle POQ is a right triangle and hence Pythagoras Theorem gives

(y + 4)2 + (x + 4)2 = 202

Substitute x = 16/y and simplify. I got

y4 + 8 y3 - 368 y2 + 128y + 256 = 0

I then used Mathematica to solve the quartic equation and got four solutions which numerically are

y = 1.04, y = 15.35, y = -23.72 and y = -0.67

From the diagram the result you are looking for is y = 15.34 which symbolically is

y = 2(-1 + Sqrt[26] + Sqrt[23 - 2 Sqrt[26]]) where Sqrt is the square root.

Thus the length you want is

4 + 2(-1 + Sqrt[26] + Sqrt[23 - 2 Sqrt[26]])

which is approximately 19.35 meters.

Penny