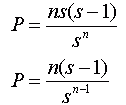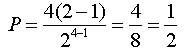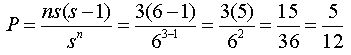From: Kalyan

I am a kind of person who do maths & statistics because I love these subjects. I came to know about your site from internet. Right now I am working on probability & number theory.

I have one question. Could you please help me. Here is my question:

Q. When four people toss fair coins, what is the probability that in a given toss there will be one "odd man". That is one person whose coin does not have the same out comes as that of any other members?

Hi Kalyan.

We can easily write out all the possibilities and just identify how many there are with an "odd man" and divide that by the total number of possibilities:

So you can just read off the probability in this case, but what about a more general approach where the numbers are too big to use this simplistic approach?

Since each toss (and coin) is "fair", there is an equal likelihood of it turning out as heads or tails. This means there are two equal possibilities. Let s = 2.

Each toss is entirely independent of the others. That means the outcome on one toss has no bearing on the outcome of another toss. There are four independent tosses, so let n = 4.

Now the number of different four-toss outcomes is the number of choices for each toss multiplied together. This is sⁿ .

That gives us the total (because 2⁴ = 16, just as in our table). Now we can take a look at the events we really want to count: how many have an "odd man" out. We can interpret this as meaning that everyone except one person gets the same outcome.

Let's say that n-1 people get heads. How many choices does the last toss have, if it cannot be the same?

It could be anyone who gets it, so that means there are n possible people who didn't throw heads. How many non-heads outcomes can one toss have? s-1.

That means the number of four-toss outcomes with everyone getting heads except for one person is n(s-1). But this is only one of the s cases, so really there are s times this many odd-man out situations. That makes the total number of equally-likely outcomes ns(s-1). The probability, P, is this divided by the total sⁿ:

Let's check this with the original four-coins question:

So the formula we came up with works for this situation. Let's test it on one other situation. Let's say 3 people roll fair six-sided dice (one each). What is the likelihood of an "odd man" situation?

In this case, n = 3 people and s = 6 sides, so we predict:

Is this accurate? The numbers are still small enough for us to write out the possibilities: