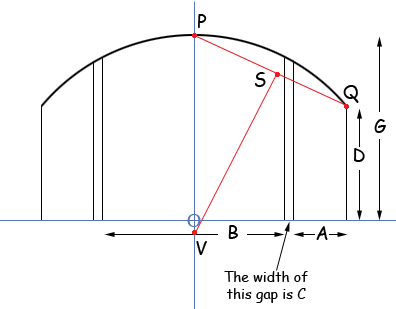
I need to calculate Dimension E and F. I am given A, B, C, (or over all A+B+C), D, G. The radius is one continuous unknown radius.
Example: A = 23.50”
B = 35.50”
C = 0.50”
D = 11.50”
G = 23.50”
I have calculated this for angles but my mind is drawing a blank for the radius calculation. I can draw it but I need to put into Excel spreadsheet.

Thanks for your assistance,

Kaye

Hi Kaye,

I redrew the diagram you sent based on out email conversation, and labeled some points.

I drew a coordinate axis with the origin at O, the midpoint of the line of length B. V is the centre of the circle and lies of the y-axis. Since P and Q are on the circle the centre must lie on the right bisector of the line segment PQ. Hence I am going to find the equation of this right bisector and see where it crosses the y-axis. This will give me the centre and radius of the circle from which you should be able to determine the other dimensions you need.

P has coordinates (0,G) and Q has coordinates ( ^B/₂ + C + A, D) and hence S the midpoint of PQ has coordinates

( ^{(B + 2C + 2A)}/₄ , ^{(D + G)}/₂)

The line through P and Q has slope

 ^{(2D - 2G)}/_{(B + 2C + 2A)}

and thus the right bisector of the line segment PQ has slope

 ^{(B + 2C + 2A)}/_{(2G - 2D)}

Thus the right bisector of the line segment PQ has equation

y - ^{(D + G)}/₂ =  ^{(B + 2C + 2A)}/_{(2G - 2D)} (x -  ^{(B + 2C + 2A)}/₄ )

This line intersects the y-axis at V which has x-coordinate 0 so the y-coordinate of V is

y  =  ^{(B + 2C + 2A)}/_{(2G - 2D)} (0 -  ^{(B + 2C + 2A)}/₄ ) +  ^{(D + G)}/₂

= - ^{(B + 2C + 2A)2}/_{(8G - 8D)} +  ^{(D + G)}/₂

With the example dimensions you sent I got V to have coordinates (0, -55.12) and hence the radius of the circle is 23.5 + 55.1 = 78.6".

Harley