Dear Math Central,
I'm a creative type who needs to find how you can determine the horizontal, relative percentages within a triangle. Attached is a pdf showing approximately the
50% line, but I'd like to know how to determine any percentage (horizontally) within a triangle . I know that if I put a horizontal line though the height of the triangle I won't be showing 50% above and 50% below. The bottom part has to be larger (correct me if I'm wrong).

I'm not concerned about height as I am wanting to break down the percentages into 60% at the bottom, 25% in the middle and 15% at the top.

Thanks in advance for your help.

Sincerely,
Ken

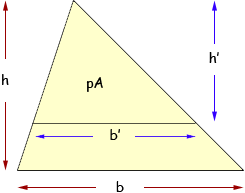
Hi Ken,

I produced a diagram much like the one you sent and then I put some labels on it.

The initial triangle has base of length b and height h so the area is given by

A = ¹/₂  b h

The horizontal line cuts off a certain proportion of the area above the line. I want to call this proportion p. (I would rather work with proportions than percentages.) The horizontal cut-off line is of length b' and the triangle above this line has height h'. Thus the area of the triangle above the cut-off line is given by

pA = ¹/₂  b' h'

Substitute A from the equation above to get

p ¹/₂  b h = ¹/₂  b' h'

Thus

p b h = b' h' or
p = ^b'/_b  ^h'/_h  

The original triangle and the triangle above the cut-off line are similar so

 ^b'/_b =  ^h'/_h 

and hence

  p = ^h'/_h  ^h'/_h  = (^h'/_h)²

Finally

h' = √p h

Thus in your example you want 15% of the area above the cut-off line so p = 0.15 and √0.15 = 0.39. Thus draw the cut-off line so that the height of the triangle above the cut-off line is 39% of the height of the original triangle.

The next cut-off line is to leave 40% of the area of the original triangle above it so here p = 0.40 and √0.40 = 0.63. Thus draw the next cut-off line so that the height of the triangle above this cut-off line is 63% of the height of the original triangle.

Penny