Name: ken
Who is asking: Other
Level of the question: All

Question: I am trying to make an octagon shaped soffit in my ceiling and need help figuring how to divide the circle on the ceiling into an octagon-
The circle is 7 foot in diameter.

 

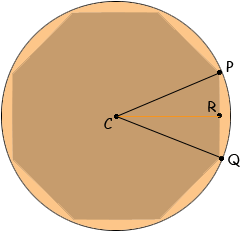
Hi Ken,

If you draw lines from the vertices of the octagon to the centre of the circle you subdivide the octagon into eight congruent triangles, one of which, PCQ, is in the diagram below.

Since there are 8 triangles the measure of the angle PCQ is 360/8 = 45 degrees. Also the length of PC is 3.5 feet.

R is the midpoint of QP so the measure of the angle PCR is 22.5 degrees. The sine of the angle PCR is  |PR|/|PC| and hence

|PQ| = 2 |PC| sin(22.5) = 7 sin(22.5) = 2.6788 feet, which is approximately 2 feet 8 1/8 inches.

Penny