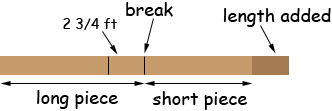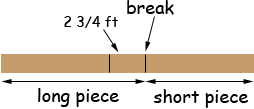
Name: Kenneth
Who is asking: Other
Level of the question: All

Question: Hello:

Here is my question: A pole 22 5/6 feet long is broken in two. One piece is 2 3/4 feet longer than the other. What is the length of each piece?

Hint: How much added to the shorter would make it equal to the longer? Adding this to the pole would give what total length?

I am especially interested in knowing how to determine the answers by using the information provided to help determine the answers.

I thank you for any helpful reply that may be sent to me.

 

Hi Kenneth,

I think the point of the first hint is that if you knew the length of the shorter piece then the length of the longer piece would be the length of the shorter piece plus 2 3/4 feet.

To say this algebraically, if the length of the shorter piece is x feet then the length of the longer piece is x + 2 3/4 feet.

I am not sure what the second hint is trying to say but the first is enough. If you know the length of shorter piece then you can find the length of the longer piece and add them to get the length of the pole. That is

x + x + 2 3/4 = 22 5/6

Can you solve this equation for x? Let us know if you have difficulty completing the problem.

Penny

Kenneth wrote back

My follow-up question is as follows:

Can the answer be determined without using the algebra calculation that you used? The section of the book that I saw this question in does not involve algebra. The section pertains to adding and subtracting fractions. I am curious to know how the answer can be determined by simply adding and subtracting fractions.

Kenneth,

Now I understand the second hint.

In the diagram the length of the longer piece is the length of the shorter piece plus 2 3/4 feet. Adding this length (2 3/4 feet) to the pole gives a length of

22 5/6 + 2 3/4 feet.

On the diagram this becomes

Now look at the extended pole in the diagram above. To the left of the break the length is the length of the long piece. To the right of the break the length is the length of the short piece plus 2 3/4 feet, but this is the length of the long piece. Thus

twice the length of the long piece is 22 5/6 + 2 3/4 feet

and hence

the length of the long piece is one half of 22 5/6 + 2 3/4 feet.

Penny