I need to find out how to calculate the square footage of an area in my backyard that is in the shape of a "slice of pie". There are two sides that are straight lines that come together at the top to form a point, and then at the bottom is a curved line that joins the two other lines together. I need to figure out how to calculate the square footage that is inside the area.
Your assistance with this is appreciated.

My name is Kim
I don't know the age group for this question, I am guessing secondary.
I am neither a student nor a teacher.

Thanks again,

Kim

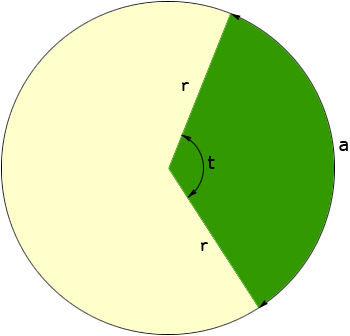
Hi Kim,

I am going to assume that the two straight line sides of your lot are the same length and that the curved side is a piece of a circle. If this is not true then the calculation of the area is much more difficult.

Suppose that you draw the entire circle with centre where the two straight sides intersect and radius the length of the straight sides. In my diagram the green section (a sector of the circle) represents your backyard, r is the length of the straight sides, a is the length of the curved side (an arc of the circle) and t is the angle measurement in degrees.

The area of the entire circle is r² and the area of the sector is a fraction of r² . In fact the area of the sector is the same fraction of the area of the circle as the size of the angle t is of 360 degrees. That is

area of the sector = r^{2  (t in degrees)}/_{(360 degrees)}

This is the conventional way to calculate the area of a sector but it requires that you measure the angle t. Unless you have a survey of your lot or a transit this is difficult to measure.

If you have a flexible measuring device and can measure the length a of the arc (the length of the curve at the bottom of your backyard) then there is another way to calculate the area. To do this I am going to use the fact that the circumference of a circles is 2 r. Using the same reasoning as I did with the area, the length of the arc is the same fraction of the circumference of the circle as the size of the angle t is of 360 degrees. That is

length of the arc a = 2 r  ^{(t in degrees)}/_{(360 degrees)}

Solve this equation for t to get

t = ^{(360 a)}/_{(2 r)}

If you now substitute this expression for t into the expression for the area of the sector and simplify you get

area of the sector = ¹/₂  a r

I hope this helps,
Penny