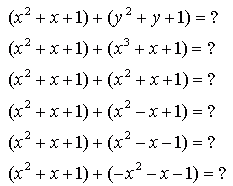From: Kris

I have a question regarding polynomials.

Suppose that two polynomials, each containing 3 terms, are added. Is it possible for the sum to contain more than 3 terms? fewer than 3 terms? exactly 3 terms? Explain.

 

We have replies to your question from two people. Here they are:

Hi there,

When adding polynomials together, the secret is combining like terms. Like terms are terms that have exactly the same variable(s) with exactly the same exponent.

Ex. 5x2 and -2x2 are like terms
  -4x and 12y are not like terms

If the two trinomials being added together have no like terms or at most 2 pairs of like terms, then the resulting sum will have more than 3 terms.

Ex. (5x2 - 2x + 3) + (4y - 7y2 +4y3 ) = 5x2 - 2x + 3 + 4y - 7y2 + 4y3 (6 terms)
  (5x2 - 2x + 3) + (4y - 7y2 + 5) = 5x2 - 2x + 4y - 7y2 + 8 (5 terms)
  (5x2 - 2x + 3) + (3x2 + 4y - 2) = 8x2 - 2x + 4y + 1 (4 terms)

If the two trinomials being added together have like terms that match one for one in them, and none of them are additive inverses of each other, you get an answer with exactly 3 terms.

Ex. (4x2 + 5x - 8) + (x2 - 7x +3) = 5x2 - 2x - 5

If the two trinomials being added together have like terms that match one for one in them, and there are additive inverses involved, you get a 0 term that is not written in the sum, resulting in fewer than 3 terms.

Ex. (6x2 - 4x +3) + (2x2 + 4x + 3) = 8x2 + 6

(- 4x and + 4x are additive inverses that result in 0x)

Hope this helps,
Leeanne

Hi Kris. I can reply to your question with my own questions:

How many terms do the following sums of three-term polynomials have?

Hope this helps!
Stephen La Rocque.