I assume this is a secondary class problem.

re: a circle - need to find area of a circle between a given line (cord) to the circumference of the circle (see attachment). I often review blue prints of homes and many times have to know the area the home.

Thank you for your help.
Larry

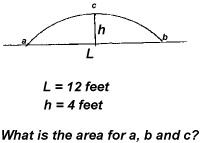
Hi Larry.

We reproduced the diagram you sent

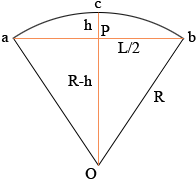
If you draw radii from the center of the circle to the end points of the chord, you will have a circular sector (a pie slice). The lines we've drawn, together with the chord itself, forms an isosceles triangle (since two sides are radii of the circle). So if we can get the area of the circular sector (pie slice) and subtract the area of the isosceles triangle, we'll have the area of the shape you are seeking (it mathematics we call that a circular segment).

Working in radians, the area of a circular sector is 1/2 R s, where s is the arc length. The arc length is of course just the vertex angle of the sector (the angle aOb formed by the two radii), which we'll call theta, times R, making the area of the circular sector 1/2 R² theta.

The area of the isosceles triangle aOb is 1/2 base times height, which is L/2 (R-h)

So if we subtract these, we get A = 1/2 R² theta - L/2 (R-h).

What remains is to determine R and theta from the information you have, L and h. The triangle bPO is a right triangle so from Pythagoras theorem

R² = (R-h)² + (L/2)²

Expand and solve for R to get

R = L²/(8h) + h/2

For your example L = 12 feet and h = 4 feet so

R = L²/(8h) + h/2 = 144/32 + 2 = 6.5 feet

From the diagram sin(bPO) = L/(2R) so

theta = 2 arcsin(L/(2R)) = 2 arcsin(12/13) = 2 1.176 = 2.35
(make sure you use radians)

Thus the area you want is

A = 1/2 R² theta - L/2 (R-h)
= 1/2 6.5² 2.35 - 12/2 (6.5 - 4)
= 49.64 - 15 = 34.64 square feet

Hope this helps!
Stephen and Penny