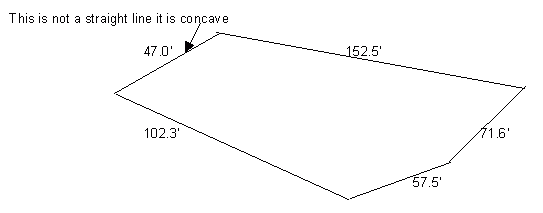
Question from Liz:

I have a square footage question. I'm looking at buying a piece of land and would like to know how to calculate the square footage of it. The lot is a very odd shape and I have attached a drawing of the lot:

This is all the information that I have and since I do not own it yet I am unable to provide more. I'm not sure if this is sufficient.

Thank you in advance for your assistance.

Hi Liz.

I'm afraid I'm the bearer of bad news: that's not enough information to determine the area of the lot.

Here's why: imagine that each of your lines is a stick and each corner is a hinge joining two sticks. Do you have a figure that can change shape? Yes, you do, even though the length of the individual sticks (sides of the lot) are constant.

You need at least two of the five possible "diagonals" (any of the two, in fact) in order to fix the locations of all the corners and thereby have a definite shape whose area you can compute.

One alternative would be an accurate drawing that reveals what the actual angles are (or is "close enough" for your purposes). At least one pair of adjacent angles would need to be accurately known to go about it this way.

I had hoped your drawing would be close enough to make an estimate, but the numbers you've given tell me that it can't be close (for example, your 71' side is drawn shorter than the 47' side).

If you can get any additional measurements, or can scan in the land survey (hopefully that is available to you from your municipality if you are considering purchase of the lot), then we can solve it for you.

Stephen La Rocque.>

Liz wrote back.

Hi Sue/Harley,

I see where my drawing was incorrect. I've scanned the plan to Word and
attached a copy I hope this will help.

Thank you in advance
Liz

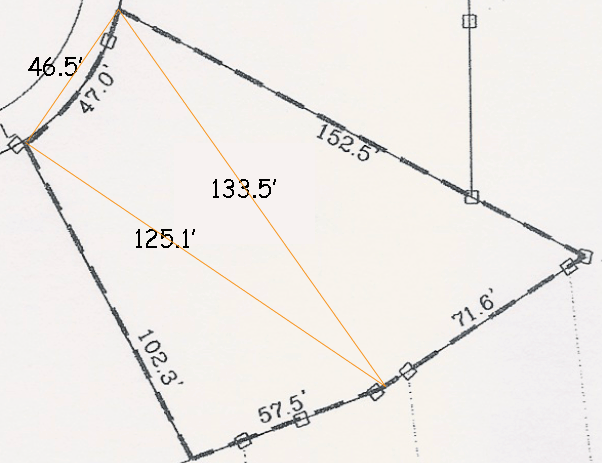
Hi Liz,

I took the drawing you sent and drew in some additional lines in orange and then, based on the drawing I estimated the lengths of these lines.

Now I have your piece of land divided into three triangles, except for the concave side. I then used Heron's Formula to find the area of each of the triangles and got a total area of 10590.6 square feet. A rough approximation of the area eliminated by the concave side is 140 square feet and hence the area of your piece of land is approximately 10450 square feet.

Harley