From: Lori

A 12-foot ladder is leaning across a fence and is touching a higher wall located 3 feet behind the fence. The ladder makes an angle of 60 degrees with the ground. Find the distance from the base of the ladder to the bottom of the fence.

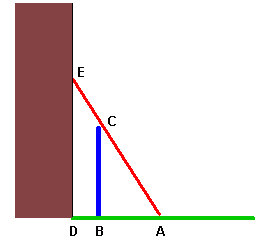
Hi Lori.

The first thing I always do with geometry puzzles is try to sketch a diagram of what's going on and then I label important points on it.

The red line is the ladder, the blue line is the fence, the building is brown and the ground is green. Let's make the pretty normal assumption that the building and the ground are at right angles.

We're given that CBA (which is also EAB) is 60°, BD is 3 feet and AE is 12 feet. We want to find AB.

The first thing to notice is that we are dealing with similar right triangles. In a right triangle, if you know the length of one side and one of the acute angles, you can calculate anything else you want about that triangle. When we look at the EAD, we see that AD = BD + AB, so if we can calculate AD, we'll be able to solve the problem.

In this triangle, you can use Cosine to find AD. The cosine of an angle in a right triangle is equal to the length of the short side adjacent to the angle over the hypotenuse. That means cos(EAB) = AE / AD.

Hope this helps!
Stephen La Rocque.