 |
 |
|
From: Lori I have a pizza. The radius is 10 inches long.The pizza was cut into 16 equal slices. When one slice was left, my sister and I both wanted it, so we agreed to cut it in half, but I like the crust more than she does, so we decided to cut it the "other way." In other words, the two pieces would not be symmetrical. The inside piece would contain all topping, and the outer piece would contain some topping and some crust. Finally, the question: How far up the radius from the center of the circle will I need to cut so we will both have an equal area of pizza? Note: The area of the crust and topping make no difference. Just think of it as a regular circle.
|
|
Hi Lori. Here's a sketch of the pizza slice:
We want to find the distance CD that will make the area of The area of a circle is πr2, but we are only interested in this 16th of it. So if the radius is 10 inches, the total amount of pizza to be divided in half is 1/16π102 = 19.63 inches2. Each person gets half of this, so that means your sister's triangular piece Notice that The area of a triangle is half the base length times the height. In the right triangle The Tangent function gives the ratio of the opposite side over the adjacent side of a right triangle. That means that in our case, tan(11.25°) = AD/DC. That means AD = (DC)tan(11.25°). Now we can use this expression in the calculation of the area of Let's set x = DC (just for simplicity): From here, all that's left is to solve for x. Hope this helps!
|
 |
 |
 |
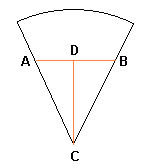 I've drawn a couple of orange lines and labelled some points as well.
I've drawn a couple of orange lines and labelled some points as well.