Hi. Please can you help me with the following problem.
One circle (circle 1) of radius 7cm is touching another circle (circle 2) of radius 4cm. (The radii are marked vertically on the circle). These circles are on a line and the problem is to find the length AB where A is the point marking the end of the radius of circle 1 and B is the point marking the end of the radius of circle 2.
I know that the circle makes a 90 degree angle with the circle (tangent property), but I am still struggling! I have tried using pythagoras, but to no avail!
Please help.
Many thanks
Louisa
Hi Louisa.
I think the diagram I've drawn below is what you are describing. I've added (in blue) my own lines that will help.
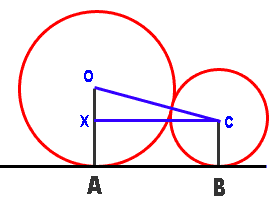Recall that when two circles are touching each other, there is a straight line between their centers which is the sum of the two radii. That means that the length of line segment OC is 4+7=11 cm. The line CX that I've drawn is perpendicular to OA. That means you can calculate the length OX by subtracting the radii. Now you have a right triangle OXC with two sides known. If you use Pythagorus to solve for the length CX, then you've also solved the length AB because the bottom shape is a rectangle.
Recall that when two circles are touching each other, there is a straight line between their centers which is the sum of the two radii. That means that the length of line segment OC is 4+7=11 cm. The line CX that I've drawn is perpendicular to OA. That means you can calculate the length OX by subtracting the radii. Now you have a right triangle OXC with two sides known. If you use Pythagorus to solve for the length CX, then you've also solved the length AB because the bottom shape is a rectangle.
