| |
|
Name: Majeedah
Who is asking: Student
Level of the question: Secondary
Question: I'm upgrading thru correspondence and haven't been in school for a long while, so I have no class or teacher to explain the basics to me.
I have a couple of questions:
The problem is this:
-
f(x) = x2 - 2, Find the expression.
Q f(-x)
A x2 - 2
Why is the answer not -x2 - 2?
-
A relation f, is given by f(x) = x - 2/x. Find the expression.
Q 2/f(3)
A 6
How do you get the answer.
|
|
|
Majeedah,
-
What this means is you need to substitute "-x" for all values of "x"
in the expression:
f(-x) = (-x)2 - 2
but since (-x)2 = (-x) 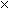 (-x) and the product of two negative numbers is positive, (-x) and the product of two negative numbers is positive,
(-x)2 = x2. By convention, when we simplify this expression we drop the minus sign because it is simpler to write x2 than (-x)2. Hence f(-x) = x2 - 2.
Writing -x2 - 2 is not the same as (-x)2 -2 because the order of operations (look up "BEDMAS" in our search form for more information on this) says that the x2 must be evaluated before the minus. For
example, if x is 2, then
-22 - 2 = - 2 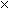 2 - 2 = -4 - 2 = -6, but (-2)2 - 2 = (-2) 2 - 2 = -4 - 2 = -6, but (-2)2 - 2 = (-2) 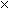 (-2) - 2 = 4 - 2 = 2. (-2) - 2 = 4 - 2 = 2.
-
Replace x with 3 to find f(3):
f(3) = 3 - 2/3.
Put that under 2 to find 2/f(3):
2/f(c) = 2 / (3- 2/3)
Now you simplify the left-hand side to get the answer:
2 / (3 - 2/3) = 2 / (7/3) = 2 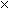 (3/7) = 6/7 (3/7) = 6/7
Clearly the answer is not 6, but 6/7.
I'm guessing that you forgot some parentheses. If f(x) = (x-2) / x then
f(3) = (3-2) / 3 = 1/3
and so
2 / f(3) = 2 / (1/3) = 2 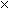 (3/1) = 6. (3/1) = 6.
Hope this helps,
Stephen La Rocque.
|
|
|
|




