 |
 |
|
From: Malissa, a secondary-school student What is the measure of the interior angles of a decagon? |
|
Hi Malissa. Let's think about this in general. Any time you walk all the way around an object and come to your starting point, you've gone around it once. That's a full circle which is 360 degrees. But here we are looking at the exterior angles. For a pentagon, it looks like this:
You can also see that each interior angle is the supplementary angle of the course correction (the two add up to a straight line). That means that for each corner, there is an interior angle of 180 - Ec degrees, where Ec is the exterior angle at that corner. So the total degrees of all the interior angles is: (180 - E1 ) + (180 - E2 ) + (180 - E3 ) + ... + (180 - Ep ) where p is the number of points in the polygon (10 for a decagon, 5 for a pentagon). We can re-write this as: 180p - (E1 + E2 + E3 + ... + Ep ) But isn't the part in parentheses just the total of the exterior angles? We know that is 360! So the total of the interior angles is just: 180p - 360 for any polygon. If the polygon is a regular polygon, then all the angles are the same, so just divide this total by the number of corners of the polygon to get the size of each interior angle. Hope this helps! Stephen really appreciates the help she got on this problem from Walter Whiteley's answer to a similar problem we received a while ago. By typing in polygon on our search page, she found Walter's earlier answer and many other problems. If you try our search page before sending us a question, you may find your answer right there and you won't have to wait for us to reply to one that you type in and send to us.
|
 |
 |
 |
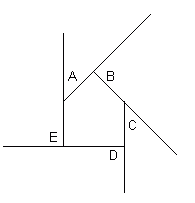 In this drawing, I've arbitrarily chosen a house-shaped polygon. Each of the letters can be interpreted as a "course correction" as we walk around. Start from the lower left corner and you see that you need to make a course correction of A = 45°, B= 90°, C = 45°, and D and E = 90° each. That adds up to 360°, as we expected. Note that if we had a convex polygon, we'd be subtracting at those angles where the course corrections go left instead of right.
In this drawing, I've arbitrarily chosen a house-shaped polygon. Each of the letters can be interpreted as a "course correction" as we walk around. Start from the lower left corner and you see that you need to make a course correction of A = 45°, B= 90°, C = 45°, and D and E = 90° each. That adds up to 360°, as we expected. Note that if we had a convex polygon, we'd be subtracting at those angles where the course corrections go left instead of right.