 |
 |
|
From: Mark, a student Question: Hello, I'm having trouble with a problem and wanted to see if someone could give me an example of this problem? I have a 3 pulley system with sides abc and pulleys ABC. Pulley A has radius of 10cm, pulley B has radius of 20cm, and pulley C has radius of 3cm. The side lengths are: (center to center of pulleys) between pulleys AB = 75cm, between pulleys BC = 100cm, and between pulleys AC = 50cm. I set these side lengths up as (according to law of sines and cosines) a = 100cm, b = 50cm, and c = 75cm. What is the length of the belt required for this system? I need to know how I would set this problem up and solve. Thank you. |
|
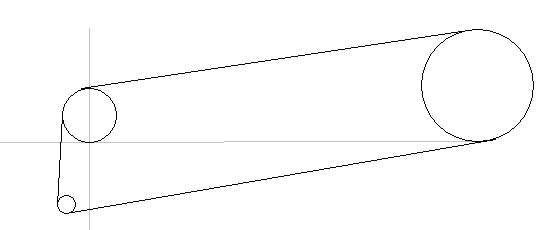
Hi Mark. This is a fairly involved problem. I will show you my way to solve it, although there may be other approaches. First I drew a diagram in a cartesian plane with a rough estimate of where things are:
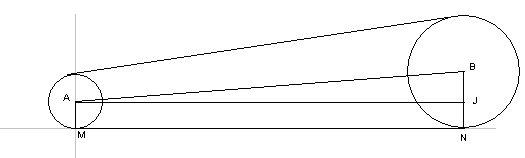
As you can see, I've placed pulleys A and B "on" the x-axis. This will make my calculations easiest. I can calculate the lengths of the straight segments using Pythagorus' theorem and use simple trig calculations to figure out the angles involved, which will tell me where the belt meets each pulley. But this gets complicated with three pulleys, as the symmetries are a little more subtle. We'll start by considering the two pulley system A and B, because (i) it's simpler and (2) the numbers we acquire are the same as we need to solve the ABC three pulley system. Take a look more closely as a two-pulley system AB. I'll draw some extra lines and label some points:
A and B are the centers of circles A and B, respectively. AJ is parallel to MN, which overlays the x-axis. Since the belt is tangent to both circles, the distance MN is the actual belt from tangent point to tangent point, so we want to calculate its length. We are given that circle A has radius 10 and circle B has radius 20, so AM = BJ = JN = 10. We are also given that AB is 75 units. By using Pythagorus then, AJ must be : Note now the symmetry: since line AB connects the centers, it must be the axis of symmetry of the system, so when we draw the other side:
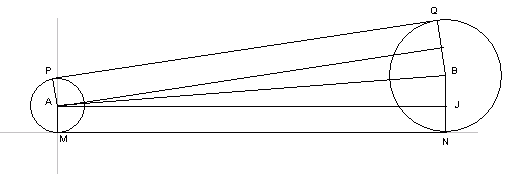
we can see that PQ must equal MN, which we've already calculated. You can do this for each of the three straight segments of the belt by laying our your pulleys in this way, a pair at a time. The next part of the puzzle is to determine the length of belt that is in contact with each pulley, that is, the arc lengths joining the straight segments. Clearly, the key here is to figure out the angles involved. Let's start by examining
You can also see from the diagram, that I think from here, the process should be clear for you, Mark. You can use this method to find the angles between centers of circles and the tangent points, then, using the fact that there are 2 Add them all up and you have your answer. Hope this helps,
|
BAJ (let's call it 
): 
radians in a circle, calculate the subtended arc angles at each pulley. Since the arc length is simple r
, where r is the radius and  |
 |
 |