From: Marlene

Which of the basic functions is related to the geometric sequence:
Linear, Quadratic, Rational, or Exponential?

Can you give me an example of how it would be used in normal life?

Hi Marlene.

I've drawn below a graph of the shapes of the basic functions: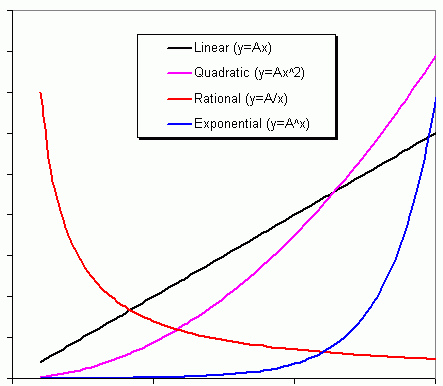

and here is a graph of some points in a geometric sequence { 2, 4, 8, 16, 32, ... }:

Can you look at this graph and see what characteristic shape it is similar to in the first graph?

Here's another way to think of it. An exponential function, at its simplest, is in the form y=A(C^x) where A and C are just constants. A geometric sequence is one that is defined by the form a_n = a₁(R^n-1) where a₁ and R are just constants. Look similar? They should, because a geometric sequence is just the discrete form of an exponential.

You asked where you might use this in normal life. You just have to think of situations where something increases (or decreases) by a certain ratio at a constant rate. For example, compound interest means that the amount increases (if you are a saver) or decreases (if you are a borrower) at a set ratio, such as 5% each year. So in this example, a₁ would be your initial investment or loan and R is the rate at which it compounds (1.05). Assuming there are no payments or withdrawals, the a_n term represents the total amount after n years.

Hope this helps!
Stephen La Rocque.