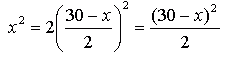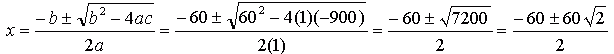|
 |
|
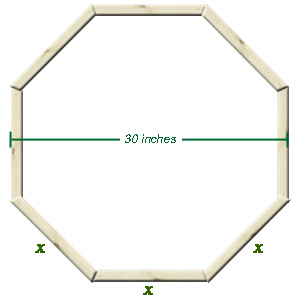
From: Martin I would like to make an octagon out of 2x4 lumber. I know that the lumber needs to be cut at 67.5 degree angles, but how do I determine the length of each piece if I want to make, say, a 2.5 ft diameter octagon?
|
|
Hi Martin. I'll assume that we'll talk about outside dimensions throughout. Let me draw a diagram to get us started:
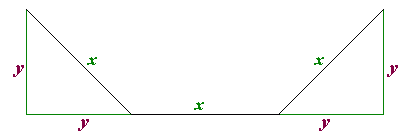
Now x is the length we are trying to determine. I'll draw a geometric model that will help us do the mathematics:
The bottom length is the same as the width of the octagon (30 inches). That means that 30 = x + y + y which you can re-arrange as y = (30 - x)/2. The Pythagorean theorem tells us that the square of the hypotenuse of a right triangle equals the sum of the squares of the two legs. In our diagram, that means x2 = y2 + y2 . If we substitute our expression for y from above, we get this:
Now we have to re-arrange this so that we can figure out the value of x. 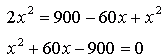 This gives us a quadratic equation we can't easily factor, so we'll use the Quadratic Formula to find the value of x:
Which reduces to: 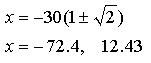 Now, obviously, that piece of wood won't be -72.4 inches long! But the other length, 12.43 inches is just what we want for the 30 inch octagon. In fact, if you you work it out, so if want a "formula" for your carpentry for other sizes of octagons, use this: where w is the outside width of your octagon. Hope this helps!
|
 |
 |
 |