|
 |
|
In a certain normal distribution, find the mean when the standard deviation is 5 and 5.48% of the area lies to the left of 78.
|
|
Mary, I think that drawing a diagram helps clarify what is being asked. This is a normal distribution so the curve is "bell-shaped" but you don't know the mean
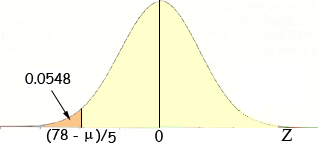
To use the area under the curve value, 0.0548, you are going to need to use the standard normal table so you need to convert X to the standard normal variable Z. You know the standard deviation is 5 so the transformation is
and the diagram becomes
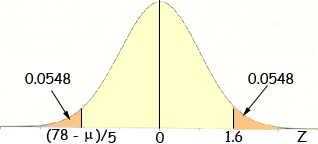
Now I need to find 0.0548 in the standard normal table. My table reads areas to the right of the value so when I look for 0.0548 I find a Z-value of 1.6
Since the normal distribution is symmetric about the mean
Solve for Penny |
 |
 |
 |
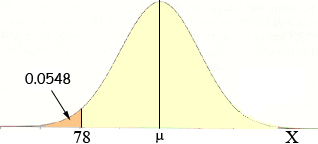
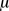 so you can't place the Y-axis. The area under the curve is 1 and the area under the curve to the left of 78 is quite small, 5.48%, that is 0.0548, so 78 must be quite far to the left. I am going to use X for the random variable.
so you can't place the Y-axis. The area under the curve is 1 and the area under the curve to the left of 78 is quite small, 5.48%, that is 0.0548, so 78 must be quite far to the left. I am going to use X for the random variable.