Assume that blood pressure readings are normally distributed with a mean of 120 and standard deviation of 8. A researcher wishes to select people for a study but wants to exclude the top and bottom 10 percent. What would be the upper & lower readings to qualify people to participate in the study?
Please help, my answer is 99 & 131, I figured this by drawing a picture, but I'm not sure if I did it correctly. Thank you.

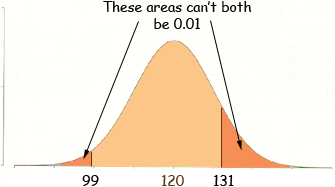
Hi Mary,

The normal distribution is symmetric about the mean. You know this from the bell-shaped curve. Your top limit of 131 is 11 points above the mean (131 - 120 = 11) and your bottom limit 99 is 21 below the mean (120 - 99 = 21).

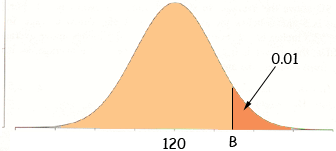
It is clear from the diagram that the area under the curve above 131 can't be the same as the area under the curve below 99 and hence there must be an error in your solution.

You need to find the value B of blood pressure so that the area under the curve above B is 10%, that is 0.01.

As in the question you sent us earlier you need to convert this value B to the standard normal distribution using

Z = ^{(X - )}/  = ^{(B - 120)}/ ₈

Using the standard normal table look up the value on the Z-axis that cuts off an area of 0.01 to the right. Set that value equal to  ^{(B - 120)}/ ₈ and solve for B.

Penny