Meadow
secondary (10-12))
student

Suppose that a submarine has been ordered to follow a path that keeps it equidistant from a circular island of radius r and a straight line shoreline that is 2 units from the edge of the island. Derive an equation of the submarine path, assuming that the shoreline has equation x = -p and that the center of the island is on the x-axis.

please help me with this problem, i really don't understand what i have to do

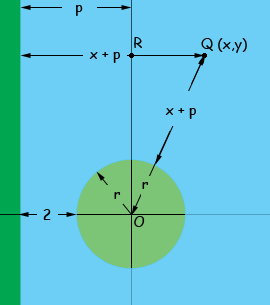
Meadow,

I started to draw a diagram of the situation you describe and I realized that the center of the island is on the x-axis, but I have a choice as to where on the x-axis it is. I decided to place the center of the island at the origin, so here is my diagram.

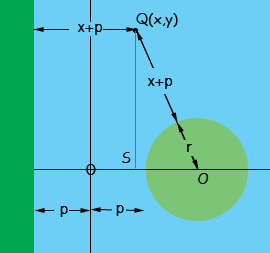
The green circle with center at the origin is the island, the shoreline is P units to the left of the origin, The distance from the island to the shoreline is 2 units and the radius of the island is r units. I let Q, with coordinated (x,y) be a point on the path of the submarine. (I put Q in the first quadrant, you need to check the equations in each of the 4 quadrants.) The distance from Q to the shoreline is x + p units so the distance from Q to the island is x + p.

Look at the diagram. QRO is a right triangle so by using Pythagoras Theorem you can find a relationship among the lengths of the sides of the triangle where |QR| = x and |RO| = y. This gives you a relationship between x and y that involves r and p. Again from the diagram, p = r + 2 so you can simplify this relationship to involve only x, y and r.

Penny,

hello again I'm really sorry, but the problem had a typo in it. its supposed to be 2p units from the edge of the island, not just 2. i looked at the problem now, and it doesn't change things that much, does it?

suppose that a submarine has been ordered to follow a path that keeps it equidistant from a circular island of radius r and a straight line shoreline that is 2p units from the edge of the island. Derive an equation of the submarine path, assuming that the shoreline has equation x = -p and that the center of the island is on the x-axis.

Meadow,

The idea is still the same but now I know where the centre of the island must be. Since the shoreline is at x = -p and the shoreline is 2p units from the edge of the island, the island is a circle with centre O at (p + r, 0). My diagram changes to

Now the right triangle is QSO with |QS| = y, |OQ| = x + p + r and |SO| = p + r - x. Apply Pythagoras theorem and simplify.

Penny

Hello again. sorry, this is concerning the submarine problem again. you've really helped me a lot with this problem, but i'm sorry, i still don't understand the last part. it says to derive an equation for the submarine path. if the submarine was to be equidistant from the shoreline and the island, wouldn't its path be a parabola? i don't understand what the Pythagorean theorem has to do with it. it gives you an equation with p, r, x, and y. how does this help get an equation?

-Meadow

Hi Meadow,

Yes I agree that the curve is a parabola, but how do you know this? The points on a parabola are equidistant from a point and a line but the point on this curve are equidistant from a circle and a line. I can see two ways to show that this is a parabola. One is the method I showed you. If you use Pythagoras theorem it gives an equation with p, r, x and y as you noted. If you simplify this equation you will see that it is the equation of a parabola.

The second method is to draw the line x = - p - r, that is a line parallel to the shoreline and r units onshore. A point on the curve with coordinates (x,y) is a distance of x + p + r from this line and a distance of x + p + r from the centre of the island. Hence the curve is a parabola with focus at O, the centre of the island, and directrix the line
x = -p -r.

Penny