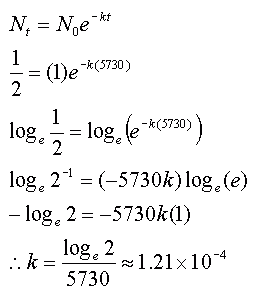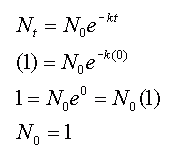|
 |
|
Question: The graph of an exponential function passes through the points (0,1) and (4,10) find the constant of growth or decay. State the function. I know that this is some kind of log problem. can you guys please help?
|
|
Hi Meadow. Yes, this is related to "log" problems. An exponential function is actually the inverse of a logarithm function and the two kinds of problems often use both concepts in their solutions. Exponential functions involving decay or growth generally follow this model:
where Nt is the amount of something you have in the time t after you start with an initial amount N0. The k is the decay or growth constant that governs how fast things grow or shrink over time. It's a principle that is used frequently in science. For example, the "half-life" of a radioactive substance is the time it takes for half of it to decay into simpler particles. Carbon-14, 14C, is a naturally-occurring radioactive isotope of carbon that accumulates in the bodies of animals while they breathe. It has a half-life of 5730 years. What that means from a practical sense is that if I find the remains of prehistoric human and I want to figure out how old it is, I can measure the ratio of carbon-14 that is present in the remains and compare that to what a living human would have. If I found the ratio was about one-eighth, the I could conclude that this person died about 17300 years ago because 5730 years ago the ratio would be double today's value (making it 1/4), 5730 years before that it would be four times today's value and 5730 years before that it would be about the same as today's living creatures. Radiocarbon dating, as this is called, uses the standard form of an exponential decay rate to infer how long something has been dead. If we say that the normal, living ratio of 14C is N0 and for convenience, we say that that is just 1, then in 5730 years (t = 5730), Nt would be 1/2. Pretty quickly then, we can work out the decay constant for Carbon-14:
Do you see how I did that? I used the normal properties of logarithms and exponents to solve the equation for k, the decay constant. (Note, some people are more familiar with the notation ln in place of loge - they mean the same thing: the "natural" logarithm). Now let's understand your question in this context: The graph of an exponential function passes through the points (0,1) and (4,10) find the constant of growth or decay. State the function. You are given coordinates and asked to find the function. Coordinates are really just pairs of variables. For a given x, a function gives you the y value. So just as correctly, for a given t, an exponential function can give you the Nt. You still need to figure out N0 and k, though. Let's look carefully at the data points you are given: If the pair is interpreted as (t, N0) then you can see that this is an exponential growth rather than decay because when one of them increased, the other increased. If you substitute the point (0,1) into the equation model, you get:
So that figured out the N0 value and putting that together with the other data point is all we need to solve for the constant of growth. Just substitute in the point (4,10) and N0=1 and solve for k following the idea I showed earlier. Hope this helps!
|
 |
 |
 |