|
Meadow
Secondary Student
Hello. I have a question that was assigned, but i really don't understand how to do it.
I was wondering if you guys could help me.
Here's the question.
5 sailors plan to divide a pile of coconuts among themselves in the morning. During the night, one of them decides to take his share. After throwing a coconut to a monkey to make the division come out even he takes 1/5 of the pile. The other four sailors repeat this procedure, each throwing a coconut to the monkey and taking 1/5 of the remaining coconuts. In the morning the 5 sailors throw a coconut to the monkey, and divide the remaining coconuts into 5 equal piles. What is the minimum number of coconuts that could have been in the pile originally?
I am totally clueless of how start so please help!
thanks!
~Meadow
|
|
Meadow,
Let n be the number of coconuts initially.
The first sailor throws 1 to the monkey, leaving n-1 coconuts. This is divided into 5 equal piles, and the first sailor takes 1 pile, leaving 4 piles. That is, the first sailor takes 1/5 and leaves 4/5 of n-1. Thus, after the first sailor, the number of coconuts is 4/5(n-1) = (4/5)n - 4/5.
The second sailor throws 1 to the monkey, leaving (4/5)n - 4/5 - 1 coconuts. This is divided into 5 equal piles, and the second sailor takes 1 pile, leaving 4 piles. That is, the first sailor takes 1/5 leaves 4/5 of
(4/5)n - 4/5 - 1. Thus, after the second sailor, the number of coconuts is (4/5)[(4/5)n - 4/5 - 1] = (4/5)2 n - (4/5)2 - 4/5
Similarly, after the third sailor, the number of coconuts is
(4/5)[(4/5)2 n - (4/5)2 - 4/5 - 1]
= (4/5)3 n - (4/5)3 - (4/5)2 - 4/5
Similarly, after the fourth sailor, the number of coconuts is
(4/5)[(4/5)3 n - (4/5)3 - (4/5)2 - 4/5 -1]
= (4/5)4 n - (4/5)4 - (4/5)3 - (4/5)2 - 4/5
Similarly, after the fifth sailor, the number of coconuts is
(4/5)[(4/5)4 n - (4/5)4 - (4/5)3 - (4/5)2 - 4/5 - 1]
= (4/5)5 n - (4/5)5 - (4/5)4 - (4/5)3 - (4/5)2 - 4/5
= [(45)n]/(55) - 4^5/55 - (44) 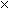 5/55 - (43) 5/55 - (43) 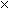 (52)/55 (52)/55
- (4^2) 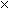 (53)/55 - (4) (53)/55 - (4) 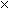 (54)/55 (54)/55
= [1024n]/3125 - 1024/3125 - (256) 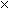 5/3125 - (64) 5/3125 - (64) 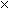 (25)/3125 (25)/3125
- (16) 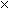 (125)/3125 - (4) (125)/3125 - (4) 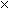 (625)/3125 (625)/3125
= 1024n/3125 - 1024/3125 - 1280/3125 - 1600/3125
- 2000/3125 - 2500/3125
= 1024n/3125 - 8404/3125
In the morning, the sailors give 1 to the monkey, leaving
= 1024n/3125 - 8404/3125 - 1
= 1024n/3125 - 8404/3125 - 3125/3125
= 1024n/3125 - 11529/3125
This is divided into five equal piles, so each sailor gets:
(1/5)(1024n/3125 - 11529/3125)
= 1024n/15625 - 11529/15626
= (1024n - 11529)/15625
This number must be a whole number, so
1024n - 11529 is a multiple of 15625
In other words, there is a whole number k, such that
1024n - 11529 = 15625k
Solving for n gives
n = (15625k + 11529)/1024
n = 15625k/1024 + 11529/1024
n = 15k+ (265k/1024) + 11 + (265/1024)
n = 15k + 11 + 265(k+1)/1024
n = 15k + 11 + 5 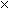 53(k+1)/(210) 53(k+1)/(210)
We must find the smallest k such that the equation above gives a whole number answer for n. In other words, we must find the smallest k such that 5 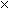 53(k+1)/(210) is a whole number. 53(k+1)/(210) is a whole number.
But 5 is not divisible by 2, and 53 is not divisible by 2. Therefore, (k+1) must be divisible by 210.
So, the minimum value of k that works will come from:
k+1 = 210
Hence, k = 1024 - 1 = 1023
Recall:
n = (15625k + 11529)/1024
Therefore,
n = (15625 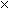 1023 + 11529)/1024 = 15621 1023 + 11529)/1024 = 15621
Therefore the minimum number of coconuts is 15621.
Check that answer works:
First sailor: 15620/5 = 3124
15620 - 3124 = 12496 coconuts left after the first sailor.
Second sailor: 12495/5 = 2499
12495 - 2499 = 9996 coconuts left after the second sailor.
Third sailor: 9995/5 = 1999
9995 - 1999 = 7996 coconuts left after the third sailor.
Fourth sailor: 7995/5 = 1599
7995 - 1599 = 6396 coconuts left after the fourth sailor.
Fifth sailor: 6395/5 = 1279
6395 - 1279 = 5116 coconuts left after the fifth sailor.
In the morning, there are 5116 coconuts. Give 1 to the monkey, leaving 5115 coconuts. 5115/5 = 1023. We always get a whole number, so the answer works.
|




