From Meghan, a secondary school student

Hi Math Central.

I've got a picture that should help you understand what I'm asking:

Given: radii of congruent inscribed circles is 1. Find the radius of the large circle

Thanks for your help!
-Meghan

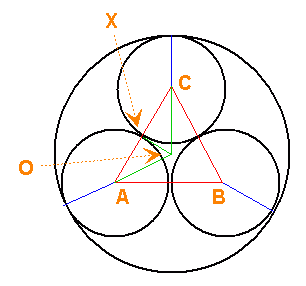
Hi Meghan.

To help solve this problem, I've re-drawn your picture with some helper lines and labelled some points in the diagram.

All the blue lines are radii of the small circles (you are given that this is 1 unit). The small circles are tangent to each other, so the orange lines connecting their centers are just two radii end-to-end. What is a bit trickier is to find the length of OC, the distance between the top small circle's center and the center of the large circle. Once you have OC, you just add 1 to it to get the radius of the large circle.

Take a good look at the orange triangle. By symmetry, it should be clear to you that this is an equilateral triangle. That means all its angles are 60°. Dig a bit deeper into the geometry and you see that the line OC bisects ACB, so XCO must be half that: 30°.

You can also see that XOC must be a right triangle again because of symmetry. Now you know the angles of the right triangle XOC as well as the length of one side.

At this point, you can use simple trigonometry to solve for the length OC: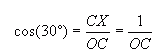

Hope this helps!
Stephen La Rocque >