|
Hi Neal,
By symmetry you need to do is find the intersection of a cylinder and a plane with inclination 45 degrees. Cylindrical coordinates (r, 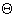 , z) give a nice development. Equation of cylinder is r=r0. Equation of plane is z = x, i.e., z = r cos , z) give a nice development. Equation of cylinder is r=r0. Equation of plane is z = x, i.e., z = r cos 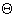 . Intersection of two surfaces is (r0, . Intersection of two surfaces is (r0, 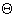 , r0 cos , r0 cos 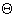 ). Already parameterized by theta, so unroll it and voila, you have a graph of one complete phase of cosine. :-) ). Already parameterized by theta, so unroll it and voila, you have a graph of one complete phase of cosine. :-)
For your application, you only need a quarter of the unrolled cylinder for half of the upper half of a tunnel, so you need cosine from its minimum to the point where it crosses the axis and then back down again, i.e. half a period of -r0 |cos 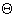 |. If you're cutting the thing out of strips of paper, the amplitude of the |cos| function should be width of paper/ |. If you're cutting the thing out of strips of paper, the amplitude of the |cos| function should be width of paper/ . .
I created a template for one vault with a radius of 5 cm. If you print this make sure you turn off all scaling. The width of the template should be approximately 15 cm. If you want a different radius then let us know.
Ed
|




