|
 |
| Name: peter Who is asking: Other Level of the question: All Question: given a straight line. how do i work out the off sets ( at right angles) at several intermediate points. to set out a 5.0m arc that has a 18.0m radius. thanking you in advance
|
|
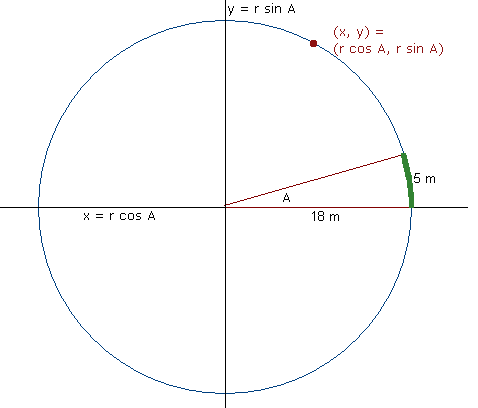
Peter, We have two responses for you, one from Stephen and the second from Penny. Hi Peter. I've graphed a circle of radius 18 m with the center at the origin of the graph and I've sketched in the 5 m long arc.
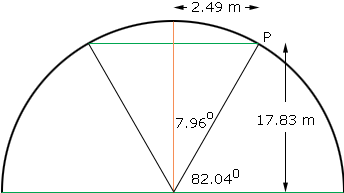
The first thing to recall is that with any circle whose center is at the origin of the graph, ALL points on a circle are in the form (r cos A, r sin A) where r is the radius and A is the angle starting from the rightwards arm and swinging counter-clockwise. You'll see I've labelled it on the diagram. You know the radius r is 18 m, so if you can determine the angle A, then you can simply put in varying numbers between 0 and A to get a sampling of intermediate points along the arc section you are interested in (I've colored it green in the diagram). To figure out A, we think about what portion of the circle our arc describes. We know that the circle's radius is 18 m, so its circumference is 2pi times that: about 113.1 m. And 5 over 113.1 is about .0442, so we are describing 4.42 % of the circle. Now a circle is 360 degrees all the way around, so 4.42% of 360 degrees is 15.92 degrees. That's A. Now you can simply calculate some values for (x, y) to get the sampling of data points you are looking for. Just calculate points from the formula: (18 cos t, 18 sin t) where t is an angle between 0 anf 15.92 degrees, Hope this helps, Hi Peter, I rotated Sue's diagram to put the arc at the top and divide Sue's 15.92 degrees by 2 to get 7.96 degrees and then found 90 - 7.96 = 82.04 degrees. Thus the point P has coordinates
Here is a blowup of the arc above the straight line.
The equation of the circle is
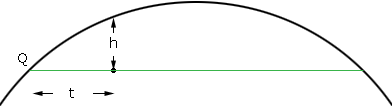
and hence to find the height of an off set (h) measure t meters from the left end of the line and calculate
where Sqrt is the square root. For example if t = 1 m then
Penny |
 |
 |
 |